初等数学公式集/初等幾何
平面図形
三角形
三平方の定理

- 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、以下の関係が成り立つ。:
- 三角形の三辺の長さa,b,cがを満たすとき、この三角形は長さcの辺を斜辺とする直角三角形となる。
(参考) 三平方の定理
正弦定理
において、, 外接円の半径を とすると、
(参考)正弦定理
正弦定理の応用

一辺とその両端の角の大きさがわかっている時の、他の辺及び当該三角形の既知の辺に対する高さ(三角測量の原理)。
- 右の図において辺が既知である時、
-
- ,
余弦定理
において、 とすると
第一余弦定理
第二余弦定理
(参考)余弦定理
中線定理とスチュワートの定理

- 中線定理
- 三角形の辺 の長さを とする。辺 上の中点 を取り、 を とすると、以下の式が成り立つ。
-
- 別形: (なお、)
-
-
- (証明)
- として、第2余弦定理より、
- 、従って、 - ①
- 同様に、
- 、従って、 - ②
- ①、②から、
- として、第2余弦定理より、
- (証明)

- スチュワートの定理
- 三角形の辺 の長さを とする。辺 上に点 を取り、 を とする。 の長さを とすると、以下の式が成り立つ。
- が辺の中点()のとき、この式は中線定理の式に一致する。
三角形における正接の性質
において、 とすると
メネラウスの定理・チェバの定理

- メネラウスの定理
- 任意の直線とにおいて、直線との交点をそれぞれとする。この時、次の等式が成立する。
- チェバの定理
- において、任意の点をとり、直線と、と、との交点をそれぞれとする。この時、次の等式が成立する。なお、点は、三角形の内部にあっても外部にあってもよい。
 |
 |
三角形の5心
重心
- 三角形の頂点から相対する辺の中点に対して下ろした線分のことを中線という。各々の頂点から下ろした線分は一点で交わり、その点を重心(通常、で表記される)という。
- 重心は中線を角側から見て、2:1 に内分する。
- (参照:ベクトルによる表記)
 |
外心
- 三角形の3つの辺の垂直二等分線は1点で交わり、その点を外心(通常、で表記される)という。
- 外心は、三角形の外接円の中心である。= 外心から各角との距離は等しい。
- (参照:ベクトルによる表記)
 |
 |
内心
- 三角形の3角のそれぞれに対して角の二等分線を取ったとき、それぞれの直線は1点で交わり、その点を内心(通常、で表記される)という。
- 内心は、三角形の内接円の中心である。= 内心から各辺との距離は等しい。= 内心から内接円と辺の接点とを結ぶ線分は内接円の半径であり、辺に対して垂直。
- (参照:ベクトルによる表記)
 |
 |
垂心
- 三角形の各頂点から対辺またはその延長に降ろした垂線は、1点で交わり、その点を垂心(通常、で表記される)という。
- (参照:ベクトルによる表記)
 |
傍心
- 三角形の2つの外角のそれぞれの二等分線と、残りの1つの内角の二等分線とは、一点で交わり、その点を傍心という。
- 傍心は各々の頂点に対する辺の反対側に存在するため、3個存在する。
- 傍心から、それに相対する辺までの距離を半径とする円は、相対する辺以外の各辺を延長した直線と接し、この円を傍接円という(下図参照)。
- (参照:ベクトルによる表記)
 |
5心相互の関係

- オイラー線
- 三角形の外心・重心・垂心は同一の直線上にある。この直線をオイラー線という。
- 右図において、
- 青の線の交点が垂心
- 橙色の線の交点が重心
- 緑の線の交点が外心
- であって、は一直線上(赤線)にある。
- 右図において、

- 垂心の性質
- に関して、と辺に対して反対側に、四角形が平行四辺形となるような点をとる。同様にに対する点、に対する点をとり、の各辺が中線となる(と相似比1:2の三角形)を得た時、
- の垂心は、の外心となる。

- 三角形の内接円と傍接円
- 傍心は三角形の二等分線上にあるので、三角形の相対する角と内心の同一直線上にある。
- 三角形の内心は、3つの傍心で作る三角形の垂心に一致する。
多角形
- 角形の内角の和:
- 角形の対角線の本数:
円
- 半径の円の円周:
- 半径、中心角(度)の扇形の弧の長さ:
- 半径の円の中心点と弦との距離をとしたときの弦の長さ:
中心角と円周角

- 円周上の点の各々から円の中心点に線分を引いた時、を中心角という。
- 円周上の点の各々から、円周上の点に線分を引いた時、を円周角という。
- 円周角の定理
- 円周上にとる点の位置に関わりなく、円周角の大きさは対応する円弧※を含む扇形の中心角の大きさのみに依存し、以下のように表わされる。
- ※:対応する円弧:ならば、円周上の点は、線分から見て中心と同じ側にあり、ならば、逆側にある。
-
- 右図において、
- 円周角とは等しい。この時の中心角の大きさをとすると、。
- 円周角とは等しい。この時の中心角の大きさをとすると、。
- したがって、円に内接する四角形の相対する角の和は、(=180°)となる。
- 右図において、
- 円周上にとる点の位置に関わりなく、円周角の大きさは対応する円弧※を含む扇形の中心角の大きさのみに依存し、以下のように表わされる。
- タレスの定理
- 接弦定理
- 三角形のある一点において外接円の接線を引いた時、接線と弦の作る角(右図において角)は、三角形の弦に対する角(右図において角)に等しい。
- 角をなす弦のではない点を、角のある点をとする。
- は、を円周角とする中心角なので、
- は、である二等辺三角形。したがって、
- において、と接線は直角をなしているから、接線と弦の作る角
- 円周角の定理
方冪の定理
- 点Pを通る2本の直線が円とそれぞれ2点と2点で交わっているとき(図1、図2):
- 円外の点を通る2本の直線の一方が点で円に接し、他方が2点で交わっているとき(図3):
 |
 |
 |
(参考) 方冪の定理
扇形
- 半径r、中心角θ[rad]の扇形について、
- 弧の長さ:
- 弦の長さ:
-
立体図形
- 縦の長さa、横の長さb、高さh の直方体の対角線 l:
- 底面の半径をr、母線の長さ lの円錐の高さ h:
- 凸面体の頂点の数をv、辺の数をe、面の数をfとすると以下の関係が成り立つ(オイラーの多面体定理):
面積と体積
平面図形の面積
解説はこちらのページをご覧ください
- 三角形
- 底辺のながさ 、高さ の三角形の面積 :
- 二辺のながさが , でその間の角が θ である三角形の面積 :
- ある辺のながさが でその両端の角が θ, δ である三角形の面積 :
-
- ※上記「正弦定理の応用」で、底辺と両端の角から高さが求められることを利用。
-
- 三辺のながさが , , で内接する円の半径が である三角形の面積 :
- 三辺のながさが , , で外接する円の半径が である三角形の面積 :
- 三辺のながさが , , である三角形の面積 :(ヘロンの公式)
- また、 とすると、
- 内接円の半径を とすると、三角形の面積
- 従って、
- 外接円の半径を とすると、三角形の面積 から
- 従って、
- 上2式から、
- 内接円の半径を とすると、三角形の面積
- また、 とすると、
- 一辺のながさ の正三角形の面積 :
- 底辺のながさ 、高さ の三角形の面積 :


- 四角形
- 縦のながさ 、横のながさ の長方形の面積 :
- 一辺のながさ の正方形の面積 :
- 底辺のながさ 、高さ の平行四辺形の面積 :
- 上底のながさ 、下底のながさ 、高さ の台形の面積 :
- 対角線のながさ 、もう一つの対角線のながさ でそれらが直行する四角形(直交対角線四角形 ⊃ 凧形・菱形・正方形)の面積 :
- 四辺の長さがで円に内接する四角形の面積:(ブラーマグプタの公式)
- また、 とすると、
- 縦のながさ 、横のながさ の長方形の面積 :
- 正多角形
- 一辺のながさ の正角形の面積 :
- 中心(重心、外心、内心)から各角までのながさ である正角形の面積 :
-
- なお、このような正角形の周の長さは、 である。
-
- 一辺のながさ の正角形の面積 :
- 円と扇形
- 半径 の円の面積 :
- 半径 、中心角(度)の扇形の面積:
- 半径 、中心角 θ(rad) の扇形の面積 :
- 半径 、弧の長さの扇形の面積 :
- 半径 の円の面積 :
立体図形の表面積等
解説はこちらのページをご覧ください
- 縦のながさ 、横のながさ 、高さ の直方体の表面積 :
- 底面積 :
- 側面積 :
- 底面積 :
- 一辺のながさ の立方体の表面積 :
- 底面の周の長さ 、高さ の柱体の側面積 :
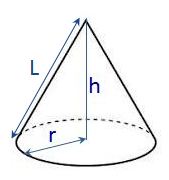
- 円錐
- 底面が半径 、母線 の円錐:
- 側面積
- 表面積 = 側面積 + 底面積
- 底面が半径 、高さ の円錐:
- 母線
- 側面積
- 表面積 = 側面積 + 底面積
- 底面が半径 、母線 の円錐:

- 直角三角錐(3直角四面体)
- 三角錐において,1つの頂点に集まる3つの角 , , がいずれも直角である三角錐
- 以下、とする。
- 頂点から、に下した垂線の長さ;
- の面積;
-
- ド・グアの定理(通称:四平方の定理)
-
- 頂点から、に下した垂線の長さ;
- 以下、とする。
- 三角錐において,1つの頂点に集まる3つの角 , , がいずれも直角である三角錐
- 半径の球の表面積:

- 球冠(平面により切断された球の一部)の曲面部の表面積:
- 関係する諸数値を以下のものとする(右図参照)。
- 球の半径
- 球冠の底の半径
- 球冠の高さ
- 球の中心から球冠の頂点(極)までの線と球冠の底を形作る円板の端との間の極角
- と を用いて、
- と を用いて、
- と を用いて、
- 関係する諸数値を以下のものとする(右図参照)。

- 球台(球を1対の平行な平面で切断した立体/先端が切り取られた球冠)の曲面部(球帯)の表面積:
- 関係する諸数値を以下のものとする(右図参照)。
- もとの球の半径
- 球台の底の半径
- 球台の高さ(2つの平行な底面間の距離)
- と を用いて、
- と を用いて、
- 球を切断する平行な2平面の外に球の中心がある場合
- (ただし、)
- 球を切断する平行な2平面の間に球の中心がある場合
- 球を切断する平行な2平面の外に球の中心がある場合
- 関係する諸数値を以下のものとする(右図参照)。

- 半径の円を、円の中心からの距離(但し、 ≦ とする)の直線を軸として回転させた円環体(トーラス、ドーナツ型) の表面積:
体積
解説はこちらのページをご覧ください




- 縦のながさ 、横のながさ 、高さ の直方体の体積 :
- 一辺のながさ の立方体の体積 :
- 底面積 、高さ の柱体の体積 :
- 底面積 、高さ の錐体の体積 :
- 円錐
- 底面が半径 、高さ の円錐の体積 :
- 底面が半径 、母線 の円錐の体積 :
- 高さ
- 底面が半径 、高さ の円錐の体積 :
- 円錐
- 上底の面積 、下底の面積 、高さ の錐台の体積 :
- 特に、上底が半径の円、下底が半径の円、高さ の円錐台の体積 :
- 特に、上底が半径の円、下底が半径の円、高さ の円錐台の体積 :
- 下底が 縦のながさ 、横のながさ の長方形、縦と平行である上辺のながさ 、高さ のくさび形の体積 :
- 一辺のながさ の正四面体の体積 :
- 一辺のながさ の正八面体の体積 :
- 一辺のながさ の正十二面体の体積 :
- 一辺のながさ の正二十面体の体積 :
- 球の体積 :

- 球冠(平面により切断された球の一部)の体積:
- 関係する諸数値を以下のものとする(右図参照)。
- 球の半径
- 球冠の底の半径
- 球冠の高さ
- 球の中心から球冠の頂点(極)までの線と球冠の底を形作る円板の端との間の極角
- と を用いて、
- と を用いて、
- と を用いて、
- 関係する諸数値を以下のものとする(右図参照)。

- 球台(球を1対の平行な平面で切断した立体/先端が切り取られた球冠)の体積:
- 関係する諸数値を以下のものとする(右図参照)。
- もとの球の半径
- 球台の底の半径
- 球台の高さ(2つの平行な底面間の距離)
- 関係する諸数値を以下のものとする(右図参照)。

- 半径の円を、円の中心からの距離(但し、 ≦ とする)の直線を軸として回転させた円環体(トーラス、ドーナツ型) の体積:
ベクトル

- 平面上または空間で大きさと向きをもつ量をベクトルという[1]。
- ベクトルが点から点に向かう有向線分で表されるとき,このベクトルをと書き,を始点,を終点という。
- ベクトルであることを示すのに、などと表記することもある。
- ベクトルの大きさは、と表記する。
- と大きさが同じで向きが逆のベクトルを逆ベクトルといい、と表記する。
- 始点終点による表記をとすると、となる。
- 大きさのベクトルを零ベクトル(ゼロベクトル)といい、と表記する。
- 大きさのベクトルを単位ベクトルといい、しばしば、と表記される。の単位ベクトルは、である。
ベクトルの演算
- 加法

- において、の終点を始点としてを引くと、となる。
- これを、
- として、ベクトルの加法を定義する。

- これは、ベクトルの終点をベクトルの始点とし、の始点からの終点までの有向線分をと理解する方法であるが、各ベクトルの始点を一致させた平行四辺形の対角線をベクトルの和と理解する方法もある。
- 以上の定義により、
- と逆ベクトル:の和は、すなわち、である。
- 減法

- 上記において、が成立していた。
- ここで、通常の計算と同様の方法でを移項すると、-①
- 逆ベクトルの定義から、
- (①の右辺) となり、①は成立し移項が可能であることが分かった。
- 実数倍(スカラー倍)

- 実数について、ベクトルを以下のとおり定義する。
- の時、は、と方向が同じで、大きさがであるベクトル。
- の時、は、と方向が逆で、大きさがであるベクトル。
- の時、は、。
1次独立
- 以下、それぞれ、零ベクトルではないベクトルについて、
- について、(は実数)であるとき、は一次独立であるといい、
- ならば、 が成立する。
- したがって、が一次独立であるとき、
- ならば、かつ である。
- 逆に、について、であるとき、ならば、は一次独立である。
- 三次元空間においても、が同一平面上にないとき、は一次独立であり、
- ならば、 が成立する。
- 逆に、について、であるとき、ならば、は一次独立であり、同一平面上にない。
ベクトルの成分表示
- ベクトルについて、平面空間であれば2個の単位ベクトル、三次元空間であれば3個の単位ベクトルを用いて以下のとおり表現できる。これを、ベクトルの成分表示といい、各々の要素を、成分、成分、成分という。
- 平面ベクトル:
- 三次元空間ベクトル:
- 成分表示でのベクトル演算
- 成分表示でのベクトル演算は、各々の成分に対しておこなう
- とすると、
- 加減算
- 実数倍(スカラー倍)
- ベクトルの大きさ
- とすると、
位置ベクトル
以下に挙げる公式で平面ベクトルで成り立つものは、三次元空間ベクトルでも成り立つ(平面ベクトルは、三次元空間ベクトルの 成分を としたもの)。
- 位置ベクトル:とする時、
- 点が、線分をに内分するならば、
- 特に、線分の中点をとし、とすると、
- において、その重心について、とすると、
- 点が、線分をに外分するならば、
- 点が、2点を通る直線上の点とした時のベクトル方程式:
- 点が、空間上の3点を通る平面上の点とした時のベクトル方程式:
- 点が、線分をに内分するならば、
三角形の5心のベクトル表示
- 三角形の五心(重心、内心、傍心、外心、垂心)の位置ベクトル は、頂点の位置ベクトル を用いて、
- 一般式:で表される。ここで は重みである。
- なお、とし、三角形の面積をとする※。
内積
- と の成す角が のとき
- (内積の定義)
- 成分表示
- 平面ベクトルの場合、, とすると、
- 空間ベクトルの場合、, とすると、
- 平面ベクトルの場合、, とすると、
- 成分表示
- (内積の定義)
- , のとき、
- , , O は原点とするときの三角形 OAB の面積 :
-
- 、ここで、 より
- 与式に代入して、
- 、ここで、 より
-
- とくに、, とすると、
- 二つのベクトル , に対し、
- よって、
- 等号成立は、実数 k があって とできるときのみ。
複素数平面
複素数の実部を横軸、虚部を縦軸にとった平面を複素数平面(複素平面、ガウス平面)、横軸を実軸、縦軸を虚軸という。
を複素数平面上にプロットした点について、点や点のように表記する。
- ベクトルとの対応
- 複素数平面を単なる実数平面と考えれば、はと対応するので、
- の絶対値は原点を基準としたときの位置ベクトルの長さと考えて
- 3点が一直線上にあるとなる実数が存在する。
- に対して、
- 点は点を実軸方向にc、虚軸方向にdだけ平行移動した点
- 点は点を実軸方向に-c、虚軸方向に-dだけ平行移動した点
- 点と点の距離は
- 一つ目の平行移動は「だけ平行移動」、二つ目の平行移動は「だけ平行移動」と表すこともできる。
- と見ればこれはベクトルの加減法そのものである。
- の共軛複素数に対して、
- 点は点を実軸に関して対称移動した点
- 複素共軛の性質
- が実数
- が純虚数
- (複号同順)
- 複素数の極形式
- 偏角をとすると
- とすると、
- ド・モアブルの定理
- n乗根
- ()
- 各は単位円周上に点を頂点の一つとする正n角形を描く。
- ()
- 各は原点を中心とする正n角形を描く。
- ()
以下、点で考える。
- 内分・外分
- Cが線分ABをm:nに内分
- Cが線分ABをm:nに外分
- 位置ベクトル・座標それぞれの公式に一致する。
- 中点・重心
- Cが線分ABの中点
- の重心を表す点について、
- 二直線のなす角
- (半直線ABを始線、ACを動径とみた正方向の回転角)
- が同一直線上が実数
- が純虚数
- 方程式の表す図形
- を満たす点zの集合は、点を中心とする半径の円。
- 円のベクトル方程式の複素数表示。
- を満たす点zの集合は、2点を通る線分の垂直二等分線。
- を満たす点zの集合は、をm:nに内分する点、外分する点をそれぞれ直径の両端に持つアポロニウスの円。
- を満たす点zの集合は、点を中心とする半径の円。
- 回転移動
- 点Bは点Aを原点中心にθだけ回転した先の点。
- 複素数と行列
- はに対応する。
- 上の回転移動の例では、θ回転を表す回転行列がであることから、これがに対応することがわかる。
- はに対応する。
脚注
- ↑ 広義には、多次元の要素を持つ存在(entity)を指し、本文のものは幾何ベクトル・空間ベクトルというが、初等数学においてはこの理解で足りる。
