高等学校理科/物理IB/運動とエネルギー

高等学校理科/物理IB > 運動とエネルギー

---

本項は高等学校理科/物理IBの運動とエネルギーの解説である。

物体の運動

物体が時間とともに、その位置をかえるとき、その物体は運動(うんどう、motion)をしている、という。 例えば、ボールを上に向かって投げ上げると、ボールは下に向かって落ちて来る。このように、物体は動かすことが出来る。このとき、ボールを投げあげたときには人間が手で物体に力（ちから、force）をかけて物体の運動のようすを変えたものと解釈することが出来る。この章では、特に物体がどのような力を受けたときにどのような運動の変化を受けるかを考察する。

日常に起こる物体の運動

現実の物体の運動においては、ただ1つの力だけで表わされるような運動は数少なく、いくつかの物体から受ける力がからみ合って物体の運動のようすが決まっていることが多い。

例えば、空気中に存在する物体に力をかけて運動させることを考えてみる。ここでは、物体はそれに力をかけている人間や道具から力を受ける。しかし、一方で物体は空気と衝突することで空気の分子から力を受けることになる。このため、一般に空気中で物体が行なう運動は、力をかけている人間が意図したものとずれる傾向がある。実際にこのような対応する力によって物体の運動の様子が大きく影響を受けるかどうかは、扱う現象の様子によって大きく変わってくる。分銅程度の大きさの物体を用いた短時間の測定なら、空気抵抗の影響は無視しても差し支えないと思われる。しかし、例えばロケットが大気圏に突入するときのロケットの運動は、空気抵抗によって大きく影響され空気抵抗の影響を無視して運動の様子を解析することは適切ではない。

このように、対象とする物体の運動の様子に伴って、どの力が重要になるかを正しく見抜くことが必要となる。

摩擦力

物体が受ける力として、空気抵抗以外に物体が接している面から受ける[摩擦力(まさつりょく、friction)がある。これは、物体の運動の方向の反対の向きに物体が接している面が物体に与える力である。通常物体をある面の上ですべらせるようにしたとき、ほとんどの物体ではすべらせた物体はすぐに静止してしまう。これは、物体に対してすべらせた面からの摩擦力が働くからである。摩擦力は物質によって大きく異なっており、例えばゴムでは非常に大きい。また、スケートリンクの氷の上で物体を滑らせると、滑らせた物体が静止すること無くいつまでも滑り続けている様子が観察される。これは、氷が極めて摩擦力を与える力が弱い物質であるからである。

水圧と浮力

水に浮かぶ物体は、物体の重さと浮力とが釣り合うときに、物体は静止する。
また、浮力の大きさは、水面から下で物体が排除した重さによる力の大きさに等しい。

更に、日常見られる物体の運動として、水などの液体の中に沈めた物体に働く水圧と浮力を扱う。物体を海の深くまで沈めると、物体は水によって全体に強い圧力を受ける。例えば、深海探査を行う船は、外壁に使う金属間の継ぎ目に大きな圧力がかかるため、その圧力に堪えられるだけの強度を持った細工をしないと、継ぎ目が砕けて船全体が水に浸かってしまう。このように水の中にある物体にかかる圧力を、水圧（fluid pressure）と呼ぶ。水圧は水の深さだけによって決まる性質があり、その圧力は水の深さに比例する。

(*注意

実際には、水圧を与える液体の密度 $\rho$ と、液体が存在する地点での重力加速度 $g$ にも比例する。数式では、水圧pは、

$p=\rho gh$

で与えられる。)

また、実際には我々の住む地表は大気の海の海底にあると解釈することが出来て、我々自身も大気自身から強い圧力を受けている。この圧力を大気圧（atmospheric pressure）という。このような圧力に耐えるため、我々の体は内側から大気圧とちょうど同じ程度の圧力になるように、大気圧を押し返している。このことによって大気圧に耐えることが出来ているのである。

このことはしかし、急激に回りの大気の圧力が下がったときに身体に変調をきたすことに通じてもいる。例としては、人間は生身で宇宙空間に出ることが出来ないことがあげられる。宇宙空間には酸素が無いことからヘルメットのようなものをつけて酸素を供給することが必要な事は確かである。しかし、宇宙空間のように極端に圧力が低いところでは、人間は、体に異常を感じると考えられる。そのため、全身を宇宙服でくまなく覆い身体の回りの圧力を地上での圧力と同じ程度に保つことが求められるのである。

また、水圧と同様に空気圧も空気の深さだけによっている。そのため、高い山に登ることによって空気圧が低くなった情况を見ることが出来る。空気圧が低くなったことの代表的な現象として、袋詰めになっている食糧などがふくらんでしまうことがあげられる。これは、回りの空気圧が下がったのに対して、袋詰めになっているものの中の圧力は変化することが出来ないので、相対的に袋の中の圧力が外の圧力より高くなったことによる。また、高山では湯を沸かしたとき沸騰の温度が100${}^{\circ }C$よりも低くなる現象も空気圧が低くなっていることによる現象である。これは、物質の沸点がまわりの物質の圧力に依存していることによる。

さて、水圧の話題に戻ると水に関してもう1つ重要な現象が存在する。水に軽い物体を沈めると、その物体はどこからか力を受けて水から浮き上がって来る。この力を浮力と呼ぶ。浮力は実際には、物体が液体から受ける水圧の差によって生じている。例えば、物体が立方体の形をしていて、ある1つの面が水面に平行な向きでその立方体を水の中に沈めたとする。このとき、立方体に水圧によってかかる力は、物体の上の面より下の面の方がより深い位置にあることから、物体には上向きの力が働くことが予想される。このため、物体には上向きの力が働きこの力がちょうど浮力に対応するものになるのである。また、今のことから浮力は、物体の高さに比例する。また、圧力に圧力を受ける面の面積をかけたものが力によって生じる力になるので、浮力自身は物体が圧力を受ける面の面積にも比例する。このため、物体にかかる浮力は、物体の体積に比例することが分かるのである。更に、より正確には物体にかかる浮力は物体が沈められている液体の密度にも比例することが知られている。そのため、これらを合わせると、物体が受ける浮力は物体が押しのけた液体の質量に比例することが分かるのである。

運動の表し方

ここからは物体の運動が人間がかける力によって制御することが出来ると 仮定する。このようなときに物体がどのような運動をするかを解析する。 このとき物体の運動は物体の位置の変化で書き表すことが出来る。 物体の位置はある時刻を取ると、その時刻に対して一意に決まる。 これは、数学的には物体の位置が時刻に対する関数と なっていることに対応する。

実際の記述は以下のようになる。 物体の位置をxで表わし、時間をtとおく。 物体の位置は時間によって変化するので、

$x=x(t)$

と表わせる。

$x=x(t)$

は、xがtの関数であるということを意味する。 それぞれの運動の様子は、関数

$x(t)$

を1つ与えることによって1つ与えられるが、この関数は通常どのようなものでも かまわない。この章では特に、慣習的によく用いられる運動について その運動がどのような式で与えられるかを考察する。

等速直線運動

一直線上を一定の速さ（speed）で同じ向きに進む運動を等速直線運動（とうそくちょくせんうんどう、linear uniform motion）という。 等速直線運動における物体の位置xを時刻tの関数で表すと、$x=vt$(vは定数)となる。 このvが速さである。

速さ

先ほどの$x=vt$の式を変形すると$v=\frac{x}{t}$となる。 この式は等速直線運動に限らず、あらゆる運動について考えることができる。

ファイル:高校物理I 等速直線運動 平均の速度.png

速さについて

ある時刻$t_1$に$x_1$の位置にあった物体が、それより後のある時刻$t_2$に$x_2$の位置に移動した。 この場合、$t_1$から$t_2$までの時間は$t_2-t_1$、$x_1$から$x_2$までの位置の変化(これを変位 displacement という.)は$x_2-x_1$である。 ここで速さvを考えると$v=\frac{x_2-x_1}{t_2-t_1}$という式が考えられる。 これを平均の速さ(mean speed)という。

平均の速さの式において、$t_2$を$t_1$に限りなく近づけていく。 詳しくは数学IIや数学IIIで習うが、これを$v=\underset{t_2\to t_1}{\lim }\frac{x_2-x_1}{t_2-t_1}$と書く。 このとき、vは一定の値をとる。これを瞬間の速さという。 単に「速さ」と書かれているときは、瞬間の速さを指すことが多い。

速度

速さが同じだからといって、全く同じ運動をしているわけではない。 たとえば、新幹線同士がすれちがうとき、普通速さは同じであるが、向きは全く逆である。 速さと向きを合わせたものを速度（そくど、velocity）という。 一般に速度のように大きさと向きを持つ量をベクトル（vector）といい、速さのように大きさだけを持つ量をスカラー（scalar）という。 ベクトルは量を表す記号、または始めの位置と終わりの位置を表す記号の上に矢印をつけて$\overrightarrow{v},\overrightarrow{AB}$のように表す。 $\overrightarrow{AB}$はAからBの向き、$\overrightarrow{BA}$はBからAの向きを表すので、大きさは同じだが、向きは全く逆である。 ベクトルの矢印は量を表す数字の上に直接付けてはいけない($\overrightarrow{0}$を除く)。 ベクトルについては数学Bで詳しく学ぶ。

等速直線運動は等速度運動とも呼べる。

• 問題例

• • 問題

時刻$t_0$に速さvで位置$x_0$から x方向に移動し始めた物体は、 時刻$t(>t_0)$にどの位置に 移動することになるか。

• • 解答

速度v一定の等速直線運動の式は、

$x=v(t-t_0)+x_0$

で与えられる。この式に直接代入すると、 時刻$t$で、この物体は

$x=v(t-t_0)+x_0$

に現れることがわかる。

相対速度

動く物体Aから観測した他の物体Bの速度のことを、Aに対するBの相対速度という。（相対速度は「そうたいそくど」と読む。 相対速度：relative velocity） このとき、観測者の速度が基準となる。 例えばトラックAとオープンカーBが一直線の道路を同じ向き（正とする）にそれぞれ30km/h, 60km/h の速さで走行している時、 トラックAの中から見るとオープンカーBは30km/hの速さで前方へ遠ざかっているように見え、 逆にオープンカーBから見るとトラックAは30km/hの速さで後方へ(-30km/hの速度で)遠ざかっているように見える。 このような相対的な速度を式にする。 Aの速度を$v_A$、Bの速度を$v_B$とすると、Aに対するBの相対速度$v_{AB}$は

$v_{AB}=v_B-v_A$

で表される。すなわち物体の速度から基準の速度を引く。

加速度

自由落下は等加速度直線運動である。

速度$\overrightarrow{v}$も時刻tによって変化する。 よって、速さのときと同じように速度の変化を表すベクトルが考えられる。 これを加速度（acceleration）という。加速度は$\overrightarrow{a}$で表す。 加速度の大きさだけをaで表すこともある。大きさは単位時間あたりの速度の変化量で定義される。

等加速度直線運動

一直線上を進む加速度が一定の物体の運動を等加速度直線運動（とうかそくど ちょくせん うんどう、linear motion of uniform acceleration）という。

• 公式

物体の加速度を$a$、基準となる時刻0での速度（初速度という）を$v_0$、時刻0での位置を原点$O$として初速度の向きにx軸をとる。この時以下の公式が成り立つ。

$v=v_0+at$

$x=v_{0}t+\frac{1}{2}a{t}^2$

$v^2-v_0^2=2ax$

• 問題例

• • 問題

時刻$t_0$に速さ0で位置$x_0$にあった物体にx方向に$a$だけの 一定の加速度を与えた。このとき、 x方向に移動し始めた物体は、時刻$t(>t_0)$にどの位置に 移動することになるか。

• • 解答

等加速度運動の式

$x=\frac{1}{2}a(t-t_0{)}^2+v_0(t-t_0)+x_0$

に代入すれば良い。 このときには、$v_0=0$が与えられているので、 上の式に$v_0=0$を代入すれば良い。答えは、

$x=\frac{1}{2}a(t-t_0{)}^2+x_0$

となる。

等加速度運動

加速度が一定の運動を等加速度運動（とうかそくど うんどう）という。 等加速度運動の例に、落下運動がある。 空中に放った物体は、重力(gravity)により、加速度を持ち落下する。 この落下の加速度を重力加速度gravitational acceleration)といい、その大きさを$g$で表す。 地球上ではおよそ $g=9.8m/s^2$ となる。 これにより、斜めに放った物体は放物線の軌道を描く。

力の性質

力の合成、力のつりあい

ある物体に向きのちがう力F1（青矢印）と力F2（青矢印）を加えると、物体に加わる合力は、図のような（F1とF2を辺とする、）平行四辺形の対角線の向きになる。

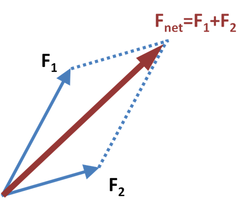
力とは、物体を支えたり動かしたりするものである。 力はベクトルで表わされる量であり、単位には [N]を用いる。[N]はニュートンと呼ばれる。 この量は、既に知られている[s],[kg],[m]を用いてかくことが出来る 単位である。実際には

[N] = [kg] $\cdot$ [m/s${}^2$]

が得られる。この関係は下で扱う運動方程式(うんどうほうていしき、equation of motion)に従う。

ここで、ある物体に対して、2つの力

$\overrightarrow{f_1}$

および

$\overrightarrow{f_2}$

が働くときに、その力は互いに足し合わされ、物体には合計で

$\overrightarrow{f_1}+\overrightarrow{f_2}$

だけの力が働く。 このように力はベクトルとしての加法則を満たすのである。

特に大きさが等しく向きが反対向きであるとき2力の合計はベクトルとして 0になり、物体に力が働いていない状態と等しくなる。このような状態を 力がつりあっているという。

• 問題

ある物体に、(I)x方向に$f$[N]、y方向に$f$[N]の力が それぞれ独立に働いているとする。 このとき、この物体には合計でどれだけの力がどの方向に働いているか計算せよ。 また、(II)それぞれの力の向きがどちらもx軸方向、 (III)片方がx軸方向でもう片方が(-x)軸 方向、 (IV)もしくは片方がx軸方向で、もう片方がx軸から測って反時計回りに 60${}^{\circ }$の方向のときにどのような力を受けているかを計算せよ。

• • 解答

(I) ベクトルの加法を用いると得られる力は

$(f,0)+(0,f)$

$=(f,f)=\sqrt{2}f(1,1)$

となる。これは、方向がx軸から測って反時計回りに45${}^{\circ }$だけ回転した方向に 等しい力で大きさは

$\sqrt{2}f$

に等しい力である。

(II) 同様にベクトルの加法を用いると、

$(f,0)+(f,0)$

$=(2f,0)$

となる。これは向きはx軸方向で大きさは2fの力である。

(III) ベクトルの加法を用いると、

$(f,0)+(-f,0)$

$=(0,0)$

となる。これは力が働いていない状態である。

(IV) ベクトルの加法を用いると、

$(f,0)+f(\frac{1}{2},\frac{\sqrt{3}}{2})$

$=f(\frac{3}{2},\frac{\sqrt{3}}{2})$

$=f\sqrt{3}(\frac{\sqrt{3}}{2},\frac{1}{2})$

となる。これはx軸から見て30${}^{\circ }$方向の力で、力の大きさは

$\sqrt{3}f$

に等しい。

運動の法則

慣性の法則

物体は外部から力が働かない限り、その速度を変えることはない。静止していた物体は、外部から力が働かない限り、静止し続ける。（自由落下運動に関しては、重力が働いているので、物体には外部から力が掛かっている。）静止している物体の速度は速度v=0だと考える

運動している物体は、外部から力がかからない限り、その速度を保ち続ける。（摩擦による速さの低下に関しては、摩擦力が物体に生じているので、これは外部から力が働いてることになる。）

物体が静止していたにせよ、動いていたにせよ、どちらにせよ、物体は外部から力が働かない限り、その速度を変えることはない。 これを運動の第一法則という。

物体の運動の、このような性質を慣性(かんせい、inertia)と言うので、この法則は慣性の法則(law of inertia)という。

運動方程式

一般に物体は力を受けたとき動きだすことが知られている。 実験の結果によると、全ての物体は ある一定の力$f$[N]を受けたとき、加速度$a$[m/s²]の大きさは、物体の受けた力に比例し、また、物体の持っている質量$m$[kg]に反比例をする。 この第二法則を式で表せば、比例係数をk₁として、

$a=k_1\frac{f}{m}$

これを運動の第二法則である。

この第二法則を力を基準に書き換えれば、比例係数をk₂として、

$f=k_{2}ma$

と表わせる。 ここで、比例係数k₂の大きさが1になるように、力の定めた単位が力の単位のニュートンである。 つまり力の単位のニュートン単位における、1ニュートンの大きさの定義とは、質量1kgの物体に力を加えた時に、1m/s²の加速度を生じさせる力の大きさを1ニュートンと定めている。

ニュートン単位を用いた力と質量と加速度との関係の方程式

$f=ma$

をニュートンの運動方程式あるいは単に運動方程式(うんどうほうていしき、equation of motion)と呼ぶ。

例えば、ある一定の力fを一様に受けている 質量mの物体は、運動方程式に従うと、 加速度

$a=\frac{f}{m}$

の等加速度直線運動をする。

• 問題例

• • 問題

質量m[kg]の物体にf[N]の力をかけたとき、 物体が受ける加速度は、何[m/s${}^2$]か。

• • 解答

運動方程式

$ma=f$

に代入すれば良い。 ここで、mは質量、aは加速度、fは力である。 ここで、両辺をmで割ると、

$a=\frac{f}{m}$

が得られ、物体が受ける加速度は、

$\frac{f}{m}[\text{m/s}{}^2]$

であることがわかる。

• • 問題

重力が存在する中で、質量mの物体を初速度$v_0$で 投げ上げた。このとき、時刻$t$での物体の位置を求めよ。 また、物体が最も高い位置に存在する時刻とその高さ、さらに 物体がちょうど地面に落ちてくる時刻を計算せよ。 ただし、物体の初期位置を$x=0$とし、投げ上げた時の 時刻をちょうど0とする。 また、重力加速度をgとする。

• • 解答

重力が物体に与える加速度は一定であるので、 この物体の運動は等加速度運動である。 このとき、物体に働く加速度は、 大きさは重力加速度gに等しく、向きはx方向の負の向きである。 ただし、x方向を物体を投げ上げた方向に取った。 よって、この物体の運動は等加速度直線運動の式を 用いて、

$x=-\frac{1}{2}g{t}^2+v_{0}t$

で表される。

ここで物体の位置xは、時刻tに関して上に凸の2次関数であるので、 必ず最大値を持つはずである。物理的には、この位置はちょうど 物体の速度が0になる位置に等しい。 上の表式を平方完成すると、

$x=-\frac{1}{2}g(t-\frac{v_0}{g})+\frac{v_0^2}{2g}$

となる。

よって、物体が最も高い位置ににいたる時刻は

$\frac{v_0}{g}$

最高点は、

$\frac{v_0^2}{2g}$

となる。

さらに、物体が地面に落ちてくる時刻は、

$x=0$

となる時刻である。

$x=-\frac{1}{2}g{t}^2+v_{0}t$

を因数分解すると、

$x=t(-\frac{1}{2}gt+v_0)$

が得られる。 この式を見ると、この物体のxはtの2次関数なのでx=0となる点は2つある。 片方は

$t=0$

であるが、これは物体を投げ上げたときの時刻なので、物体が 地面にあるのは当然である。 一方

$t=\frac{2v_0}{g}$

の方は、物体が一度投げ上げられて落ちてきたものと解釈できる。 よって、物体が落ちてくる時刻は、

$\frac{2v_0}{g}$

となる。

• • 問題

重力が存在する中、質量mの物体を 時刻0に、位置

$(x,y)=(0,0)$

から、初速度vで地面から測って

$\theta$

方向に物体を放り投げた。 物体が最高点に到る時刻とそのときの物体の位置、 物体が落ちて来るときの時刻とそのときの物体の位置をそれぞれ計算せよ。

• • 解答

物体を放った位置を

$(0,0)$

とする座標系を取り、物体が飛んでいく方向をx方向、重力が働く方向と 反対の方向をy方向とする。

このとき重力は(-y)方向にしか働かないので、物体は x方向には初速度

$v\cos \theta$

の等速直線運動をする。

また、y方向には重力が一定の大きさで働くので、 初速度

$v\sin \theta$

の等加速度運動をする。 これらを等速直線運動の公式と、等加速度直線運動の公式に代入すると、

$x=v\cos \theta t$

$v_x=v$

$y=-\frac{1}{2}g{t}^2+v\sin \theta t$

$v_y=-gt+v\sin \theta$

が得られる。ここで物体が最高点に達するときには

$v_y=0$

が成り立つので、

$v_y=-gt+v\sin \theta =0$

よって、

$t=\frac{v\sin \theta }{g}$

が対応する。一方、物体が地面に落ちたときには、

$y=0$

が対応するので、

$y=-\frac{1}{2}g{t}^2+v\sin \theta t=0$

となる。これには

$t=0,\frac{2v\sin \theta }{g}$

が対応するが、t=0は投げあげたときに対応するので、

$t=\frac{2v\sin \theta }{g}$

が対応する量である。

一方、物体が最高点に達したときの物体の位置は

$(x,y)$

にそれぞれのtの値を代入すればよい。

$t=\frac{v\sin \theta }{g}$

に対しては、

$x=v\cos \theta \cdot \frac{v\sin \theta }{g}$

$=\frac{v^2\cos \theta \sin \theta }{g}$

$y=\frac{v^2{\sin }^2\theta }{2g}$

が得られる。一方、

$t=\frac{2v\sin \theta }{g}$

に対しては、

$x=v\cos \theta \cdot \frac{2v\sin \theta }{g}$

$=\frac{2v^2\cos \theta \sin \theta }{g}$

$y=0$

が得られる。

弾性力

フックの法則。
力は伸びに比例する。

ばねなどを考えれば分かると思うが、一般に物体は形を変えるような力が働いたとき、それを押し返そうとする力を働かせる。 このように元の形に戻ろうとする性質を弾性(だんせい、elasticity)という。また弾性による復元力を弾性力(elastic force)と呼ぶ。 多くの固体の物体は、物体に加える外力が小さい場合には弾性を示す。

いっぽう、粘土のように容易に形を変えることが出来る物質も存在する。このような形を変えられる性質を塑性（そせい,plastic）という。 このように、弾性力の有無および弾性力の強さは、物質によって大きく変わる物質の性質である。

いっぽう、一般的に弾性力に関していえる現象として、形の変化が物体全体の 大きさと比べて小さいような時、物体が変形を押し返すために働かせる力は、 物体が変形した長さに比例する。これをフックの法則(Hooke's law)と呼ぶ。 例えばゴムを例に取ると、ゴムを大きく引きのばしたときに感じる力は、ゴムを小さく引きのばしたときに感じる力よりも大きい。これはゴムが引きのばされた時に発する力が、ゴム自身の変形の大きさに応じて大きくなるからである。

一般に物体が細長いときには、物体の弾性力は1本のばねで近似的に表わせる。 ここでは、特にばねについてのフックの法則を扱う。 ここでいうばねは、いくらかの長さ$l_0$を持っており、力を受けていないときには 常に$l_0$の長さを持っている。また、多くの場合ばねの質量は、他の物体の質量と比べて小さいとして、無視される。これはどちらかというと計算を簡単化するためであり、実際にはどのような物質の弾性力について考えているかにもよる。 このバネは厳密にフックの法則を満たしており、この物体の弾性力は常に物体の長さの変化の割合$l-l_0$に比例するとする。 ただし、lを引きのばされたバネの長さとした、このときの力と物体の長さの変化の割合の比例係数を、バネ定数と呼び、kとかくことにする。 このことを式でかくと、

$f=-kx$

となる。ただしここで

$x=l-l_0$

であり、この量は座標の原点をバネの端に取ったときのバネの引きのばされた大きさとなっている。xは負の量も取ることがあり、このときはバネは引きのばされるのではなく、押し潰される方向に力を受けている。

$f=-kx$

のうちの$-$符合は、バネが引きのばされるときにそれを引き返そうとする弾性力を発し、 通常より短くなるように押されるときにはそれを押し返す方向に、弾性力を働かせることに対応している。

• 問題例

• • 問題

片側を壁に固定してあるバネ定数kで自然の長さlのバネがある。このとき、(I)バネの長さが$l+l_1$になるように引きのばしたとき、バネの発する弾性力を符合も含めて答えよ。

また、(II)バネの長さが$l-l_2$となるように押し縮めたとき、バネの発する弾性力を符合も含めて答えよ。

ただし、$l_1>0$,$l_2>0$とする。

• • 解答

バネが発する力は、フックの法則

$f=-kx$

を用いて計算できる。ただし、バネの発する力の方向には注意する必要がある。

答えは、 (I)

$-k{l}_1$

(II)

$k{l}_2$

となる。

作用・反作用の法則

作用反作用の法則の例。
おもりがバネを引っ張リ下げると同時に、バネはおもりを引っ張り上げる。

バネが物体を吊り下げている場合に関して、物体が重力によってバネを引っ張った場合に、なぜ、重力を受けている物体は運動方程式にしたがって落下していかないのだろうか。それは、吊り下がっている物体が、バネを引っ張っている力と同じ大きさの力で、バネから引き上げる力を受けているからである。

このように、物体が他の物体に力を及ぼすときは、必ず相手の物体からも同じ大きさの力を受けている。これを作用反作用の法則(law of action and reaction)という。あるいは「運動の第三法則」ともいう。

磁力でも、作用・反作用の法則が成り立っている。磁石が鉄を引きつけるとき、鉄もまた磁石を引きつけているのである。

静電気の力でも、風力でも、地球の引力でも、どんな力であっても、作用・反作用の法則が成り立っている。

私たちは、地球による重力に引っ張られているが、じつは地球も、私たちによる引力で引っ張られている。これが万有引力（ばんゆう いんりょく）である。私たちが、「地球が私によっても引っ張られてる」とは感じないのは、

月は地球のまわりを回っているが、月は、地球からの万有引力を受けている。同様に、地球も、月からの万有引力を受けている。

重力の法則は、生き物かどうかとか、星かどうかとかでは影響されない。物体なら、すべての物に、万有引力は同じ法則で、作用・反作用の関係で働く。

摩擦力

摩擦力$\overrightarrow{F}$は、二つの物体の間の相対運動に反対している。図中のN_fは垂直抗力である。

摩擦力(まさつりょく、friction force)も、力の一種でありベクトルで表わされる。一般に、摩擦力には静止摩擦力と動摩擦力の2通りがあることが知られている。

静止摩擦力

静止している物体を動かし始めるのに必要な力を静止摩擦力(せいしまさつりょく、static friction force)という。物体がある物質で出来た面と接して静止しているとする。このとき物体に力をかけて物体が面に接したままで、物体を動かすことを考える。このとき、例えばゴムのような物質を考えると分かり易いが、ある程度の力をかけるまで物体が物質面からの力を受けて動きださないことがある。このように静止している物体に対して働く力を静止摩擦力(static friction force)という。 また、静止している物体を動かすにも、摩擦のため、力が余計に必要になるという、この現象を静止摩擦(static friction)という。

静止摩擦力の最大値は、物体が物質面にかける力の面に垂直な成分に比例することが知られている。このような力の垂直成分と 実際に生じる静止摩擦力の最大値との比例係数を$\mu$と書き、静止摩擦係数(せいしまさつけいすう、coefficient of static friction)とよぶ。 静止摩擦係数は物質ごとに決まる定数である。 特にこの関係を式で表わすと、

$|\overrightarrow{F}|<\mu |\overrightarrow{N}|$

のようになる。ここで、左辺の

$\overrightarrow{F}$

は摩擦力であり、右辺の

$\overrightarrow{N}$

は、物質の面に床からかかる力の垂直成分である。

物体が載っている床に物体が沈まないためには、床が物体を押し返す必要があるので、このような床からの反発力を考える必要がある。 このような床から物体に掛かる力は、床からの抗力（こうりょく、reaction）と呼ばれる。抗力とは、変形を妨げる力のことであり、床の面の接線方向に対して、抗力の方向が垂直なので、垂直抗力とよばれる。

動摩擦力

動いてる物体にかかる摩擦力を動摩擦力(kinetic friction force)と呼ぶ。 これは、物体が接している面から、物体が運動している方向と 反対の方向に働く力であり、通常物体を物質の面上に滑らせたとき、物体が 静止するのはこの力によるものである。 動摩擦力も静止摩擦力と同様に、物質の面にかかる力の垂直成分に比例した力が生じる。 しかし、同じ力の垂直成分に対しても動摩擦力の大きさは、一般に 同じ物質面を使っても静止摩擦力よりも小さい。 この現象、動いている物体の摩擦の現象のことを動摩擦(どうまさつ、kinetic friction)という。

動摩擦力の物体がかける力の 垂直成分に対する比例係数を動摩擦係数(coefficient of kinetic friction)と呼び、記号は一般に${\mu }^{\prime }$で表わす。 このことを式でかくと、

$|\overrightarrow{F}|={\mu }^{\prime }|\overrightarrow{N}|$

となる。

$\overrightarrow{F}$

は摩擦力であり、右辺の

$\overrightarrow{N}$

は、物質の面にかかる力の垂直成分である。この$\overrightarrow{N}$も垂直抗力という。

• • 問題

重力がある中に、静止摩擦係数$\mu$の物質で出来た平面を角度

$\theta$

だけかたむけて置き、その上に質量mの物体を置く。 このとき、

$\theta$

がどの大きさのとき、この物体は滑り出すか計算せよ。

• • 解答

物体は重力を受けて、鉛直下方向にmgの力を受ける。このうちで この力は斜面方向に

$mg\sin \theta$

、面に対して垂直な方向に

$mg\cos \theta$

の大きさを持っている。このとき静止摩擦力の最大値は

$|\overrightarrow{F}|=\mu |\overrightarrow{N}|$

$=\mu mg\cos \theta$

となるので、斜面方向に働く重力

$mg\sin \theta$

が

$=\mu mg\cos \theta$

よりも大きいとき、この物体は動きだすことになる。 よって、このような

$\theta$

の条件は、

$\sin \theta \ge \mu \cos \theta$

$\tan \theta \ge \mu$

となる。

エネルギー

エネルギー(energy)とは物体を動かしたり温度を上げたりできる能力を定量的に表したものである。 このようなエネルギーという量がどのような物理量を用いて表わされるかを考える。

仕事

物体に力をかけたまま力の方向に移動させることを考える。このとき、力が一定であったとする。

（力の大きさが時間的に変化する場合は、積分を使うことになるので指導要領の範囲外である。）

ここでは、物体にかかる力は常に一定であるとして考える。 力の大きさと、その力の方向と同じ方向に移動した距離との積を、物体が受けた仕事（work）と呼ぶ。 （物体が力を受けている方向とは垂直な方向に物体が動いた分については、物体は仕事をされていないと考える。）

仕事の記号は通常ではWで書かれ、その単位は

[N $\cdot$ m]

である。一方、この単位は通常

[J]

と書き換えてジュールと呼ばれる。 一般には、物体が動く方向はベクトルで表わされ、力もベクトルで表わされる。 このとき、物体が動いた量を

$\overrightarrow{x}$

物体が受けた力を

$\overrightarrow{f}$

とかくと、物体が受けた仕事は

$\overrightarrow{f}\cdot \overrightarrow{x}$

と取る。ここで、$\cdot$は、内積の記号である。例えば、物体が力を受けている方向と 垂直な方向に動いたとき、物体は仕事をされていないと考える。 例えば、重い荷物をもちあげずに運んだとき運んだ向きは物体が重力を受ける向きと 垂直であるので、物体は重力に対する仕事をされていないことになる。

実は運動方程式を用いると、物体が受ける仕事は、その物体の待つエネルギーの変化量であることが分かる。 このことを示すには、物体の持つエネルギーがどのようなものかを述べなくてはならないが、それは次の章で成される。 ただし、いずれにしても物体が受ける仕事の持つ単位と、物体の持つエネルギーの次元は同一であり、ジュールはエネルギーの単位としても扱われる。

• 問題例

• • 問題

ある物体が、x軸方向に一定の大きさの力fを受けたまま、

(I)

$l(1,0)$

(II)

$l(0,1)$

(III)

$l\frac{1}{\sqrt{2}}(1,1)$

(IV)

$l(-1,0)$

だけ動いたとする。それぞれの変位に対して物体が受けた仕事を求めよ。

• • 解答

物体が受けた力を

$f(1,0)$

として、それぞれの変位との内積を取ればよい。 (I)

$W=f(1,0)\cdot l(1,0)$

$=fl$

となる。 (II)

$W=f(1,0)\cdot l(0,1)$

$=0$

これは、物体が受けている力と物体の変位が垂直なときに対応する。 (III)

$W=f(1,0)\cdot l\frac{1}{\sqrt{2}}(1,1)$

$=\frac{1}{\sqrt{2}}fl$

(IV)

$W=f(1,0)\cdot l(-1,0)$

$=-fl$

となる。このとき、物体は負の仕事をされているという。

運動エネルギーと位置エネルギー

運動エネルギー

物体のエネルギーを定めるには、物体が他の物体を動かす力を測定するのが 順当である。 種々の実験の結果によると、ある物体ともう1つの物体が衝突したとき ぶつかった物体がぶつけられた物体を動かす力は、 ぶつけた物体の速さの2乗に比例し、ぶつけた物体の質量に比例する。 よってぶつけた物体の速さをv、質量をmとすると、ぶつけられた物体のエネルギーEは

$E=\frac{1}{2}m{v}^2$

と書ける。 ここで、係数である

$\frac{1}{2}$

は慣用的な量と合わせるためにつけている。 ここからは、質量mの物体が速度vで運動しているときその物体は

$\frac{1}{2}m{v}^2$

のエネルギーを持っているとする。運動の方向がどちらであっても、物体が持っている エネルギーは変化しない。 ここで、この量の単位を考えてみる。 この量は質量と速度の2乗の積で出来ていることから、この量の単位は

[kg] $\cdot$ [$m{}^2$/$s^2$]

=[ kg $\cdot$ m/s${}^2$]$\cdot$ [ m]

= [N] $\cdot$ [m]

となり、確かに仕事の単位と等しいことが分かる。

ここで、エネルギー

$\frac{1}{2}m{v}^2$

という量の変化が、物体が受けた仕事に対応することを示す。

ある短い時間$\mathrm{\Delta }t$の間に物体が力fを受けながら力と同じ方向に $\mathrm{\Delta }x$だけ移動したとする。 このときの物体の速度の変化を$\mathrm{\Delta }v$とすると、エネルギーの変化量は

$\frac{1}{2}m((v+\mathrm{\Delta }v{)}^2-v^2)$

$=\frac{1}{2}m(2v\mathrm{\Delta }v+(\mathrm{\Delta }v{)}^2)$

$\sim mv\mathrm{\Delta }v$

となる。ただしここで、

$(\mathrm{\Delta }v{)}^2$

の項は第1項と比べて小さいとして無視した。 この量を$\mathrm{\Delta }t$で割った量は

$=mv\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}$

となるが、ここで

$\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}$

は、物体の加速度と等しいことが予想される。 ここで、運動方程式

$ma=f$

を用いると、上の量は

$=vf$

となる。 しかしここで、

$v=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}$

であることを考えると、上の量は $\mathrm{\Delta }t$の間になされた仕事

$f\mathrm{\Delta }x$

を$\mathrm{\Delta }t$で割ったものと解釈することが出来る。 もともと始めの量は、$\mathrm{\Delta }t$の間のエネルギーの変化量を$\mathrm{\Delta }t$で割ったもので あったので、これは求めたかった結果と一致していることが分かる。

よって、物体が受ける仕事は物体の持つエネルギーの変化と等しいこと がわかった。式でかくと、

$\frac{1}{2}m(v_2^2-v_1^2)=W$

となる。ただし、ここでは物体が仕事を受ける前の速度を$v_1$, 仕事を受けた後の速度を$v_2$と取り、受けた仕事をWと取った。

このようなことから、速度vで運動する質量mの物体に対する物理量

$E=\frac{1}{2}m{v}^2$

は、運動している物体が蓄えているエネルギーと見なせる。そこで、このエネルギー量 $E=\frac{1}{2}m{v}^2$ のことを運動エネルギー(kinetic energy)と呼ぶ。

• 問題例

• • 問題

質量mを持つ物体が速度v₁で運動していた。このときその物体に ある仕事をし、その物体の速度をv₂まで引きあげた。 物体が受けた仕事を計算せよ。

• • 解答

エネルギーの変化量がなされた仕事に対応する。 よって、なされた仕事は、

$\frac{1}{2}m{v}_2{}^2-\frac{1}{2}m{v}_1{}^2$

となる。

位置エネルギー

重力加速度

質量m[kg]の物体を高さ0メートルの地面から、高さhメートルまで上げるには、重力に逆らって仕事をしなければならない。 質量1kgあたりの重力の大きさを重力加速度と言い、記号はgで表す。重力加速度gの測定値は、場所によって少しは異なるが、地球上ならば、おおむね

g = 9.8 [m/sec${}^2$]

である。（月面では、重力加速度の大きさは地球上の重力加速度よりも小さい。）

位置エネルギー

高さh[m]に持ち上げた質量m[kg]の物体は、手を離せば、重力によってmg[N]の力を受けながら、地面までの距離hの分だけ落下するので、手を話すと仕事をmgh[J]することになる。 ということは、高さh[m]にある質量m[kg]の物体はエネルギーをmgh[J]ほど持っていることになる。 このような、物体の高さによるエネルギーを位置エネルギー(potential energy)という。

位置エネルギーは物体の高さhと物体の質量mと重力加速度gに比例する。位置エネルギーの記号をUで表した場合、位置エネルギーUは

$U=mgh$

である。

運動エネルギーと位置エネルギーとの変換

次に物体をある高さから転がして、その物体の速さを測る実験を行なう。簡単化のため、物体の初速度は0とする。

このような実験の結果によると、物体の速さvは物体の元の高さhの平方根$\sqrt{h}$に比例する。

これは物体が高い位置にあることによって持っていた位置エネルギー$mgh$を、

物体の運動エネルギー$\frac{1}{2}m{v}^2$に転換したものと見ることが出来る。

• 問題例

• • 問題

高さhから質量mの物体を落とした。ここでこの物体が地面すれすれで 持つことになる運動エネルギーと速度を求めよ。 更にこの物体から全てのエネルギーを受け取った質量Mの物体は 地面すれすれの高さではどれだけの速度で動くことになるかを 計算せよ。

• • 解答

物体のエネルギーをEとすると、運動エネルギーT,位置エネルギーUとしたとき、

$E=T+U$

が成り立つ。ここで、エネルギー保存則から、高さhで物体が持っていた エネルギーと、地面すれすれで物体が持っているエネルギーは等しいことに 注目すると、物体が地面すれすれで持っている運動エネルギーは 物体が高さhで持っていた位置エネルギーと等しい。 よって、物体の地面すれすれでの運動エネルギーは

$mgh$

となる。更に、このときの物体の速度は、

$mgh=\frac{1}{2}m{v}^2$

より、

$v=\sqrt{2gh}$

となる。 また、このエネルギーを質量Mの物体が受け取ったとすると、 このときの物体の速度をVとすると、

$\frac{M}{2}{V}^2=mgh$

よって、

$V=\sqrt{2mgh/M}$

となる。

このように、エネルギーは、形をかえても、その総和は一定である。これをエネルギー保存の法則(law of conservation of energy)という。

熱と温度

落下する“おもり”の位置エネルギーを利用して、水を攪拌して場合の"温度"を調べることで、温度と位置エネルギーの関係を調べるための、科学者ジュールによる実験装置。

熱を物体に与えると、物体の温度が上がる。 また、水をかきませることで水の温度を上げることも出来る。 水をかきまぜるのは水に運動エネルギーを与えることに等しく その結果として、水の温度が上がったのである。

電気とエネルギー

発電用水車の部品。
ドイツの水力発電所の装置

発電所では、タービンを回転させることで、電気をおこしている。 これは、運動エネルギーを電気エネルギーに転換しているものと 考えることが出来る。

電気エネルギーを使って運動エネルギーに変換することも可能である。たとえば、モーターは電気エネルギーを使って運動エネルギーを 産み出しているものと考えることが出来る。

エネルギーの変換と保存

今まで見て来た通り、エネルギーには様々な形態があり それぞれは条件付で互いに変換が可能となっている。 ただし、エネルギーの総量はそれぞれの変換で 変化しないと思われている。

剛体に働く力の釣り合い

剛体に、力は、どう働く ?

てこ を使えば、100 kg の物体を 5kg の物体で持ち上げることができる。

力を加えても伸び縮みをせず、大きさを物体を剛体(ごうたい、rigid body)という。これに対して、バネなどの伸び縮みをする物体は弾性体(elastic body)という。 以下の記述では、おもに、剛体について考える。

剛体に力が掛かっている箇所を、作用点(さようてん、point of action)と言い、作用線から力の方向へ延長した直線を作用線(line of action)という。 剛体は力を加えた位置によって、動き方が異なる。力の加え方によって、並進運動の他に回転運動をする場合もある。 また、てこの原理を考えれば、同じ大きさの力を加えても、作用点の位置によって、剛体に与える影響は異なる。このことからてこの支点と作用点との距離Lと、力Fの垂直方向成分F sinθとの積を考えると好都合である。この積FL sinθを、力のモーメント(moment of force)と言う。あるいは単にモーメント(moment)という。

てこ以外の剛体に対しても、任意の点Oからの距離を考え、これを支点として、この点Oからの距離Lと力の垂直方向成分F sinθ都の積でモーメントを定義する。モーメントの単位は[N・m]である。 モーメントをMと表した場合、

M=FL sinθ

である。 剛体に掛かる力が複数個、有る場合については、その力による回転方向が基準にした回転方向と逆の場合は、マイナス符号に取る。 力のモーメントが釣り合っている場合は、モーメントの合計がゼロになり、この場合は、剛体は回転しない。

テンプレート:Clear

偶力

偶力のイメージ図

偶力

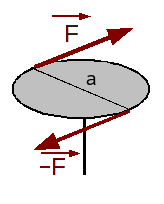
剛体に同じ大きさの力が反対方向に掛かっている場合、その力の対を、偶力（ぐうりょく、couple of force）という。

質点

剛体には大きさがあったが、この大きさを無視して、物体を質量を持った点として扱う場合は、これを質点という。 質点は、力のモーメントを持たない。

重心

重心について

(centet of grvity)

運動量と力積

運動量

運動している物体Aが静止している物体Bに衝突して、その静止物体Bを動かしたとしよう。 このとき、静止している物体が動き出す速度の大きさは、物体Aの質量m_Aが大きいほど、衝突された物体Bの速度も大きな速度で動き出すだろう。また、物体Aの速度vAが大きいほど、衝突された物体Bの速度も大きくなるだろう。

このことから、速度vで運動している質量mの物体に関して、物体の速度vと質量mの積で定められる量mvを定義すると都合がよさそうである。

物体が動いているとき、物体の速度と質量の積mvを物体の運動量(うんどうりょう、momentum)と呼び、記号は一般にpで表し

$\overrightarrow{p}=m\overrightarrow{v}$

と定義する。

運動量保存の法則

物体に対して力fを$\mathrm{\Delta }t$の間だけ 働かせたとき、

$P=f\mathrm{\Delta }t$

として、Pを力積(りきせき、impulse)と呼ぶ。 ここで、力積が運動量の変化率であることを示す。 実際ある物体に短い時間$\mathrm{\Delta }t$の間力

$\overrightarrow{f}$

がかかったとすると、

$\overrightarrow{P}=\overrightarrow{f}\mathrm{\Delta }t$

$=m\overrightarrow{a}\mathrm{\Delta }t$

$=m\frac{\mathrm{\Delta }}{\mathrm{\Delta }t}\overrightarrow{v}\mathrm{\Delta }t$

$=\frac{\mathrm{\Delta }}{\mathrm{\Delta }t}\overrightarrow{p}\mathrm{\Delta }t$

となるが、これは運動量の時間変化率

$\frac{\mathrm{\Delta }}{\mathrm{\Delta }t}\overrightarrow{p}$

に時間$\mathrm{\Delta }t$をかけたもので、運動量の時間変化に等しいことが分かる。 よって、物体にかかる力積は、物体の運動量の変化量に等しいことが分かった。

• 発展 微分と変化量

ここでは、短時間の運動量の変化率として、$\frac{\mathrm{\Delta }p}{\mathrm{\Delta }t}$という記述を用いているが、本来この量はw:微分を用いて定義される。ただし、指導要領の都合のため、ここではそのような記述はしていない。微分を用いた導出については、古典力学を参照。

• 問題例

• • 問題

静止していた物体に時間$\mathrm{\Delta }t$の間ある方向に一様な力fをかけた。物体が得た 運動量はどれだけか。更に、物体の質量をmとすると、物体がその方向に 得た速度はどれだけか。

• • 解答

運動量の変化分は物体が受けた力積に等しいので、物体が受けた力積を計算すれば よい。物体が受けた力積は

$f\mathrm{\Delta }t$

に等しいので、物体が得た運動量も

$f\mathrm{\Delta }t$

に等しい。更に、運動量が

$p=mv$

を満たすことを考えると、物体の速度は

$\frac{1}{m}f\mathrm{\Delta }t$

となる。

運動量は、物体が全く力を受けないとき保存する。 これは物体に力が働かないときには、物体の受ける力積は0であり物体の運動量 変化も0であることから当然である。

さらに、複数の物体の運動量については、別の重要な性質が見られる。それは、 複数の物体のもつ運動量の総和はそれらの物体の間の衝突に際して 保存するということである。 これはつまり、例えばある2つの物体が衝突したとき、始めに2物体がそれぞれ持っていた 運動量の和は衝突が終わった後に2物体が持っている運動量の和に等しいということで ある。 ここで、いくつかの物体があるときそれらの持つ運動量の総和を、対応する物体系の 全運動量という。

物体の衝突について、運動量は常に保存する。しかし、物体系の全エネルギーは 常に保存するとは限らない。一般に物体の衝突についてエネルギーは常に失われていく。 もっとも物体系に限らない全エネルギーは常に一定であるので、物体が持っていた エネルギーは音や熱の形で物体系の外に逃げて行くのである。物体が衝突について 失うエネルギーは衝突に関わる物体が持っている物性定数によって決まる。 この係数をw:反発係数eと呼ぶ。反発係数は、物体が衝突したする前後の 物体間の相対速度の比によって定められる。 特に物体1と物体2が衝突前に速度 $v_1$,$v_2$を持っており、衝突後に 速度${v_1}^{\prime }$,${v_2}^{\prime }$を持ったとすると、反発係数eは、

$e=-\frac{v_1-v_2}{{v_1}^{\prime }-{v_2}^{\prime }}$

で定められる。ここで、右辺の始めの$-$符合は、衝突の前後で物体の速度が より大きい物体は、衝突前により小さい速度を持っていた物体よりも 衝突後にはより小さい速度を持つことになるからである。 そのため、反発係数は一般に正の数である。 また反発係数は1より小さい数であり、物体間の相対速度は衝突前より 衝突後の方が小さくなる。特にe=1のときを完全弾性衝突と呼び $0<e<1$のときを非弾性衝突と呼ぶ。完全弾性衝突のときは、 エネルギーは失われないことが知られている。一方、非弾性衝突の ときは物体系の全エネルギーは失われる。

• 問題例

• • 問題

ある静止している物体2に運動量pで運動している物体が衝突した。このとき、 衝突した後の物体2が運動量$p_2$を得たとすると、衝突後の物体1の運動量は どれだけとなったか。

• • 解答

運動量の保存則を考えると、衝突の前後で物体1と物体2で構成される物体系の 全運動量は保存する。ここで、衝突前の物体系の全運動量はpであるので、 衝突後の物体系の全運動量もpとなる。更に、物体2の衝突後の運動量が $p_2$なので、物体1の運動量は

$p-p_2$

となる。

ここで、物体系の全運動量が保存されることは、運動に関するw:作用反作用の法則から従う。 作用反作用の法則を用いると、物体系の間の衝突に際して、衝突に関わる それぞれの物体が受ける力は、大きさが等しく向きは反対となる。 このとき、それぞれの力に対して、衝突の時間$\mathrm{\Delta }t$をかけたものは 衝突に際してそれぞれの物体が受け取る力積に等しい。ここで、 衝突に関して働く力の力積を全ての物体について足し合わせると、それらの 和は上のことから0となる。しかし、全運動量の計算ではまさにそのような 全物体についての運動量の総和を計算しているので、衝突によって得られるような 力積の総和は0に等しい。よって、衝突に際して物体系の持つ全運動量は保存される。

• 問題例

• • 問題

質量mの2つの物体が速度$v_1$,$v_2$ で移動している。これらの物体が衝突したとき、 衝突後のそれぞれの物体の速度を、エネルギー保存則と運動量保存則を用いて 計算せよ。ただし、物体の衝突に関してエネルギーは保存するとする。

• • 解答

この問題は2つの同じ大きさの物体を異なった速度でぶつけたとき その結果がどうなるかを計算する問題である。 実験の結果によると、一方が静止しており一方が動いているとき、 動いていた物体は静止し、静止していた物体は動いていた物体が持っていた 速度と同じ速度で動きだすことが知られている。ここでは、それらの 結果が計算によって確かめられることを見ることが出来る。 衝突後の物体の速度をそれぞれ物体1については${v_1}^{\prime }$,物体2については ${v_2}^{\prime }$とする。このとき、物体の衝突について全エネルギーが保存されることを 用いると、

$1/2m{v}_1^2+1/2m{v}_2^2=1/2m{v_1}^{\prime }{}^2+1/2m{v}^{\prime }{}_2^2$

が得られる。更に、物体の衝突について物体系の全運動量が保存されることを用いると、

$m{v}_1+m{v}_2=m{v_1}^{\prime }+m{v_2}^{\prime }$

これらは、$v{\text{'}}_1$,$v{\text{'}}_2$についての2次方程式であり、解くことが出来る。 実際計算すると、解として

$(v{\text{'}}_1,v{\text{'}}_2)=(v_1,v_2),(v_2,v_1)$

が得られる。前者の解は衝突に際して物体の速度が変化しないことを 示しているが、これは実際の情况として考え難いので、後者の解が現実の解となる。 この結果を見ると、物体が持つ速度が入れ替わることが分かる。

このことは実際に同じ大きさの球を用いて実験を行うと、確かめることができる。

運動とエネルギーに関する探求活動

??