高等学校数学II/微分・積分の考え

テンプレート:Pathnav ここでは微分積分の概念について理解し、多項式関数の微分積分を学ぶ。また、微分の応用を応用して接線の方程式やグラフの概形などを求めたり、積分を応用してグラフの面積を求める。微分積分は物理学や工学などさまざまな分野で応用されている。

平均変化率

平均変化率の図

中学校では、一次関数と$y=a{x}^2$の変化の割合を求めただろう。ここでは、同じものを平均変化率と呼ぶことにする。一般の関数 $y=f(x)$ の平均変化率を考えてみたい。中学校で学習したことと同様に考えると、 $y=f(x)$ において、 $x$ が $a$ から $b$ まで変化したときの平均変化率は、「 $y$ の変化量/ $x$ の変化量」で求められる。つまり、 $\frac{f(b)-f(a)}{b-a}$ である。

例

$y=x^2+2x+1$ において、 $x$ が-1から3まで変化したときの平均変化率を求める。

$\frac{(3^2+2\cdot 3+1)-((-1{)}^2+2\cdot (-1)+1)}{3-(-1)}$$=4$

極限

関数 $f(x)$ において、 $x$ が $a$ とは異なる値をとりながら限りなく $a$ に近づくとき、 $f(x)$ が限りなく $A$ に近づくことを、 $\underset{x\to a}{\lim }f(x)=A$ とかく。

例

$\underset{x\to 0}{\lim }3x$を求める。

$x$を、$1,0.1,0.01,0.001,\cdots$と限りなく0に近づけてみる。すると、$3x$は、$3,0.3,0.03,0.003,\cdots$と、限りなく0に近づくことがわかる。

よって、$x$を限りなく0に近づけると、$3x$は限りなく0に近づくので、$\underset{x\to 0}{\lim }3x=0$である。

次に、 $\underset{x\to 1}{\lim }\frac{x^2-1}{x-1}$を求める。

$x$を、$1.1,1.01,1.001,0.0001,1.00001,\cdots$と、限りなく1に近づけてみると、$\frac{x^2-1}{x-1}$は、$2.1,2.01,2.001,2.0001,2.00001,\cdots$と、限りなく2に近づく。

なので、$\underset{x\to 1}{\lim }\frac{x^2-1}{x-1}=2$である。

これは、式に値を代入する前に、式自体を約分してしまった方が簡単に計算できる。すなわち、 $\frac{x^2-1}{x-1}=\frac{(x+1)(x-1)}{x-1}$であり、$x$を1とは異なる値を取りながら限りなく1に近づけるとき$x\ne 1$なので、これは約分でき、$\frac{x^2-1}{x-1}=\frac{(x+1)(x-1)}{x-1}=x+1$である。

なので、$\underset{x\to 1}{\lim }\frac{x^2-1}{x-1}$を求めるには、$\underset{x\to 1}{\lim }(x+1)$を求めれば良い。

$\underset{x\to 1}{\lim }(x+1)=2$であるので、$\underset{x\to 1}{\lim }\frac{x^2-1}{x-1}=2$と求めることができる。

※発展　最初の例では、$x$を、$1,0.1,0.01,0.001,\cdots$と、限りなく0に近づけたが、$2,0.2,0.02,0.002,\cdots$や、$-1,-0.1,-0.01,-0.001,\cdots$のように近づけてみても$x$は限りなく0に近づく。他にも、$1,-0.1,0.01,-0.001,\cdots$や$0.1,0.5,0.01,0.05,\cdots$など$x$を0に近づかせる方法はいくらでも考えられる。

もちろん、この例では、$x$をどのように近づけたとしても極限の値は変わらない。

しかし、$x$を、$1,0.1,0.01,0.001,\cdots$と近づけたとき、$f(x)$は$\alpha$に近づくが、$x$を、$2,0.2,0.02,0.002,\cdots$と近づけたら、$f(x)$は$\alpha$に近づかない。そんな関数$f(x)$だってあるだろう。

なぜ$x$を$1,0.1,0.01,0.001,\cdots$と、近づけただけで、極限の値を求めることが出来るのか?と疑問に思う人もいるかも知れない。

極限を厳密に定義するには、イプシロンデルタ論法を使う必要がある。しかし、高校生には少し難しいと考える人が多いので高校ではあまり教えられていない。

なので、この本では、イプシロンデルタ論法を使わず、曖昧な方法で極限を定義した。なので、上のような疑問を持った人は、その疑問について深く考えずに先に進むか、イプシロンデルタ論法を学ぶかしてほしい。

平均変化率

微分係数と導関数

hを0に近づけたときのアニメーション

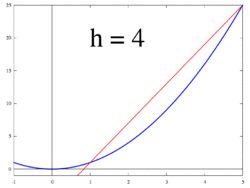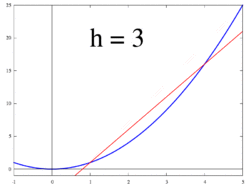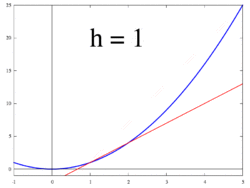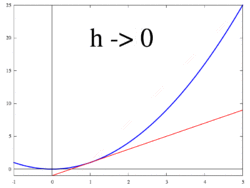
関数 $y=f(x)$ の傾きについて考えてみよう。

$x$ が $a$ から $a+h$ まで変化したときの平均変化率は

$\frac{f(a+h)-f(a)}{h}$

である。このとき、 $h$ を限りなく0に近づければ $a$ での傾きを求めることができる。つまり、関数 $y=f(x)$ の $a$ での傾きは

$\underset{h\to 0}{\lim }\frac{f(a+h)-f(a)}{h}$

で与えられる。これを $x=a$ における微分係数という。

また

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

で与えられる関数 $f^{\prime }(x)$ を関数 $f(x)$ の導関数という。

関数 $f(x)$ の導関数は$\frac{df}{dx}$と表されることもある。

ここで、いくつかの関数の導関数を求めてみよう。

• $f(x)=1$

$f^{\prime }(x)$	$=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$
	$=\underset{h\to 0}{\lim }\frac{1-1}{h}$
	$=\underset{h\to 0}{\lim }0$
	$=0$

• $f(x)=x$

$f^{\prime }(x)$	$=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$
	$=\underset{h\to 0}{\lim }\frac{x+h-x}{h}$
	$=\underset{h\to 0}{\lim }1$
	$=1$

• $f(x)=x^2$

$f^{\prime }(x)$	$=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$
	$=\underset{h\to 0}{\lim }\frac{(x+h{)}^2-x^2}{h}$
	$=\underset{h\to 0}{\lim }\frac{2hx+h^2}{h}$
	$=\underset{h\to 0}{\lim }(2x+h)$
	$=2x$

である。

$n$ を自然数とする。関数 $f(x)=x^n$ の導関数は二項定理を応用し

$f^{\prime }(x)$	$=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$
	$=\underset{h\to 0}{\lim }\frac{(x+h{)}^n-x^n}{h}$
	$=\underset{h\to 0}{\lim }\frac{(x^n{+}_n{C}_1{x}^{n-1}h{+}_n{C}_2{x}^{n-2}{h}^2\cdots +h^n)-x^n}{h}$
	$=\underset{h\to 0}{\lim }{(}_n{C}_1{x}^{n-1}{+}_n{C}_2{x}^{n-2}h+\cdots +h^{n-1})$
	$=n{x}^{n-1}$

と求められる

和・差及び定数倍の導関数

関数 $f(x),g(x)$ に対し次が成り立つ。

1. $\{f(x)\pm g(x){\}}^{\prime }=f^{\prime }(x)\pm g^{\prime }(x)$ (複号同順)
2. $\{kf(x){\}}^{\prime }=k{f}^{\prime }(x)$

証明

1. $\{f(x)\pm g(x){\}}^{\prime }=\underset{h\to 0}{\lim }\frac{f(x+h)\pm g(x+h)-\{f(x)\pm g(x)\}}{h}=\underset{h\to 0}{\lim }\{\frac{f(x+h)-f(x)}{h}\pm \frac{g(x+h)-g(x)}{h}\}=f^{\prime }(x)\pm g^{\prime }(x)$
2. $\{kf(x){\}}^{\prime }=\underset{h\to 0}{\lim }\frac{kf(x+h)-kf(x)}{h}=\underset{h\to 0}{\lim }k\frac{f(x+h)-f(x)}{h}=k{f}^{\prime }(x)$

演習問題

次の関数を微分せよ

1. $f(x)=2x^3+4x^2-5x-1$
2. $f(x)=(2x+3)(3x-5)$

解答

1.

$\begin{array}{cc}{f}^{\prime }(x)& =(2x^3+4x^2-5x-1{)}^{\prime }\\ & =2(x^3{)}^{\prime }+4(x^2{)}^{\prime }-5(x{)}^{\prime }-(1{)}^{\prime }\\ & =2\times 3x^2+4\times 2x-5\times 1-0\\ & =6x^2+8x-5\end{array}$

2. $f(x)=6x^2-x-15$ であるから

$\begin{array}{cc}{f}^{\prime }(x)& =(6x^2-x-15{)}^{\prime }\\ & =6(x^2{)}^{\prime }-(x{)}^{\prime }-(15{)}^{\prime }\\ & =6\times 2x-1-0\\ & =12x-1\end{array}$

導関数の応用

接線の方程式

曲線 $y=f(x)$ 上の点 $(t,f(t))$ における接線の方程式を求める。この接線の傾きは $f^{\prime }(t)$であり、点 $(t,f(t))$ を通るので、方程式は $y=f^{\prime }(t)(x-t)+f(t)$ で与えられる。実際、$x=t$ とすると $y=f(t)$ となるのでこの方程式は点 $(t,f(t))$ を通ることがわかり、 $x$ の係数は $f^{\prime }(t)$ なので傾きは $f^{\prime }(t)$ である。

法線の方程式

曲線 $y=f(x)$ 上の点 $(t,f(t))$ における法線の方程式は、$y=-\frac{1}{f^{\prime }(t)}(x-t)+f(t)$ で与えられる。

関数値の増減

f'(x)は、fの傾きを表わすので、 $f^{\prime }(x)>0$ の点では、fは増大し、 $f^{\prime }(x)<0$ の点では、fは減少することがわかる。

これをもとに関数の概形を描くことができる。

例

$y=x^3$ の増減を調べる

両辺をxで微分すると、

$y^{\prime }=3x^2$

となる。これは0を除き常に正なので、 $y=x^3$ は常に増加することがわかる。

関数の極大・極小

$f(x)=x^3-3x$を微分すると

$f^{\prime }(x)=3x^2-3=3(x+1)(x-1)$

増減表は次のようになる。

$x$	$\cdots$	$-1$	$\cdots$	$1$	$\cdots$
$f^{\prime }(x)$	$+$	$0$	$-$	$0$	+
$f(x)$	$\nearrow$	$2$	$\searrow$	$-2$	$\nearrow$

この関数のグラフは、$x=-1$を境にして増加から減少の状態に変わり、$x=1$を境にして減少から増加の状態に変わる。
このとき、$f(x)$は$x=-1$において極大（きょくだい）になるといい、そのときの$f(x)$の値$f(-1)=2$を極大値（きょくだいち）という。また、$x=1$において極小（きょくしょう）になるといい、そのときの$f(x)$の値$f(1)=-2$を極小値（きょくしょうち）という。極大値と極小値を合わせて極値（きょくち）という。

不定積分

不定積分(indefinite integral)とは、微分したらその関数になる関数を求める操作である。

つまり、関数$f(x)$に対して、$F^{\prime }(x)=f(x)$となる、関数$F(x)$を求める操作である。

このとき$F(x)$を、$f(x)$の原始関数(primitive function)と呼ぶ。

例えば、$\frac{1}{2}{x}^2$は微分すると、$x$になるので、$\frac{1}{2}{x}^2$は$x$の原始関数である。

しかし、$\frac{1}{2}{x}^2+1$や、$\frac{1}{2}{x}^2+3$なども微分すると$x$になるので、$\frac{1}{2}{x}^2+1$や、$\frac{1}{2}{x}^2+3$も$x$の原始関数である。

一般に、$\frac{1}{2}{x}^2+C$(Cは任意の定数)で表される関数は、$x$の原始関数である。

$x$の原始関数は一つだけではなく、無数にあるのだ。

一般に、関数 $f(x)$ の原始関数の一つを $F(x)$ とするとき、原始関数に任意の定数を足した関数 $F(x)+C$ も $f(x)$ の原始関数になる。

なぜなら、$F(x)$が$f(x)$の原始関数である、つまり、$F^{\prime }(x)=f(x)$のとき、$(F(x)+C)\text{'}=F^{\prime }(x)+{(}^{\prime }C)=F^{\prime }(x)=f(x)$となるからだ。

また、関数 $f(x)$ の原始関数の一つが $F(x)$ であるとき、すべての関数 $f(x)$ の原始関数は $F(x)+C$ の形に書ける。

$F(x)+C$ の形に書けない関数 $G(x)$が関数 $f(x)$ の原始関数であると仮定する。このとき、$h(x)=F(x)-G(x)$とすると、関数 $h(x)$ は定数ではない。

このとき、 $h^{\prime }(x)=\{F(x)-G(x){\}}^{\prime }=F^{\prime }(x)-G^{\prime }(x)=f(x)-f(x)=0$ であるはずだが、関数 $h(x)$ は定数ではないので $h^{\prime }(x)=0$ とならない。これは矛盾なので、すべての関数 $f(x)$ の原始関数は $F(x)+C$の形に書けることが証明できる。

関数$f(x)$の原始関数の全体を、$\int f(x)dx$ と表す。この表記法は最初は奇妙に思うだろうが、このように表記する理由は後に説明するので、今は、そのまま覚えて欲しい。

まとめると、関数 $f(x)$ の原始関数の全体$\int f(x)dx$は、$f(x)$の原始関数の一つを $F(x)$ として、その関数に任意の定数を足した関数$F(x)+C$で表される。つまり、

$\int f(x)dx=F(x)+C$

$C$は任意の定数としたが、この任意の定数 $C$ を積分定数(constant of integration)と呼ぶ。

※注意　$\int f(x)dx$は定義にもあるように、$f(x)$の原始関数の全体を表している。つまり、$f(x)$の原始関数の一つを$F(x)$とするとき、$\int f(x)dx=F(x)+C$の右辺$F(x)+C$は、$F(x)$に定数を足した関数の全体を表している。つまり、$F(x)+C$は、$F(x)+1$や、$F(x)-23$や、$F(x)-5\pi$などの、$F(x)$に定数を足した関数すべてをまとめて$F(x)+C$と表している。このことがあやふやになっていると、重大な間違いを起こす可能性があるので、注意が必要である。

関数 $f(x)=x^n$ (ただし $n$ は自然数)の不定積分を求めてみる。やや天下り的だが、$F(x)=\frac{1}{n+1}{x}^{n+1}+C$ ($C$ は任意の定数)とおくと、 $F^{\prime }(x)=x^n$ となるので、 $\frac{1}{n+1}{x}^{n+1}+C$ は原始関数であることがわかる。

したがって $\int x^{n}dx=\frac{1}{n+1}{x}^{n+1}+C$

関数 $f(x),g(x)$ の原始関数をそれぞれ、 $F(x),G(x)$ とする。$a$ を任意の実数定数とすると

$\{F(x)+G(x){\}}^{\prime }=F^{\prime }(x)+G^{\prime }(x)=f(x)+g(x)$

$\{aF(x){\}}^{\prime }=a{F}^{\prime }(x)=af(x)$

となるので、

$\int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx$

$\int af(x)dx=a\int f(x)dx$

が成り立つことが分かる。

演習問題

不定積分 $\int (x^8+2x^2-6x+9)dx$ を求めよ

解答

$\int (x^8+2x^2-6x+9)dx=\int x^{8}dx+2\int x^{2}dx-6\int xdx+9\int dx=\frac{x^9}{9}+\frac{2x^3}{3}-3x^2+9x+C$ ($C$ は積分定数)

定積分

関数$f(x)$の原始関数の一つを$F(x)$とする。この原始関数に値を代入して、その値の差を求める操作を、定積分と呼び、$\underset{a}{\overset{b}{\int }}f(x)dx$と書く。つまり、

$\underset{a}{\overset{b}{\int }}f(x)dx=F(b)-F(a)$

である。

$[f(x){]}_a^b=f(b)-f(a)$とする。

このようにすると、$\underset{a}{\overset{b}{\int }}f(x)dx=[F(x){]}_a^b=F(b)-F(a)$と計算できる。

定積分の値は原始関数の選択によらない。実際、原始関数として、 $F(x)+C$ を選び、定積分を計算すると、$\underset{a}{\overset{b}{\int }}f(x)dx=(F(b)+C)-(F(a)+C)=F(b)-F(a)$

となり、原始関数としてどれを選んでも定積分の値は一定であることがわかる。

関数 $f(x),g(x)$ に対して、原始関数をそれぞれ $F(x),G(x)$ とする。 $k$ を実数として、

$\underset{a}{\overset{b}{\int }}kf(x)dx=kF(b)-kF(a)=k(F(b)-F(a))=k\underset{a}{\overset{b}{\int }}f(x)dx$

$\underset{a}{\overset{b}{\int }}\{f(x)+g(x)\}dx=[F(x)+G(x){]}_a^b=F(b)+G(b)-(F(a)+G(a))=F(b)-F(a)+G(b)-G(a)=\underset{a}{\overset{b}{\int }}f(x)dx+\underset{a}{\overset{b}{\int }}g(x)dx$

$\underset{a}{\overset{a}{\int }}f(x)dx=F(a)-F(a)=0$

$\underset{b}{\overset{a}{\int }}f(x)dx=F(a)-F(b)=-(F(b)-F(a))=-\underset{a}{\overset{b}{\int }}f(x)dx$

$\underset{a}{\overset{b}{\int }}f(x)dx=F(b)-F(a)=(F(b)-F(c))+(F(c)-F(a))=\underset{a}{\overset{c}{\int }}f(x)dx+\underset{c}{\overset{b}{\int }}f(x)dx$

が成り立つ。

例

$\underset{2}{\overset{5}{\int }}{x}^{3}dx$を求める。

$\frac{1}{4}{x}^4$は、微分すると、$x^3$なので、$\frac{1}{4}{x}^4$は$x^3$の原始関数の一つである。よって$\underset{2}{\overset{5}{\int }}{x}^{3}dx={\left[\frac{1}{4}{x}^4\right]}_2^5=\frac{1}{4}{5}^4-\frac{1}{4}{2}^4=\frac{609}{4}$である。

$\frac{1}{4}{x}^4+1$も、微分すると、$x^3$なので、$\frac{1}{4}{x}^4+1$は$x^3$の原始関数の一つである。よって、$\underset{2}{\overset{5}{\int }}{x}^{3}dx={[\frac{1}{4}{x}^4+1]}_2^5=(\frac{1}{4}{5}^4+1)-(\frac{1}{4}{2}^4+1)=\frac{609}{4}$と求めることもできる。

微分積分学の基本定理

aを定数とするとき、定積分$\underset{a}{\overset{x}{\int }}f(t)dt$はxの関数になる。
関数$f(t)$の原始関数の一つを$F(t)$とすると

$\underset{a}{\overset{x}{\int }}f(t)dt=F(x)-F(a)$

この両辺をxで微分すると、$F(a)$は定数であるから

$\frac{d}{dx}\underset{a}{\overset{x}{\int }}f(t)dt=\frac{d}{dx}F(x)=f(x)$

$\underset{a}{\overset{x}{\int }}f(t)dt$の導関数

$\frac{d}{dx}\underset{a}{\overset{x}{\int }}f(t)dt=f(x)$

定積分と面積

関数$f(x)$が$a\leqq x\leqq b$の範囲で常に正であるとする。このとき、定積分$\underset{a}{\overset{b}{\int }}f(x)dx$によって、関数$f(x)$のグラフと、直線$x=a$、直線$x=b$、$x$軸で囲まれた部分の面積を求めることができる。

関数$f(x)$のグラフと、直線$x=a$、直線$x=c$と、$x$軸で囲まれた部分の面積を$S(c)$とすることによって、関数$S(x)$を定める。($a\leqq x\leqq b$とする)

関数$f(x)$のグラフと、直線$x=c$、直線$x=c+h$と、$x$軸で囲まれた部分の面積を考える($a\leqq c+h\leqq b$とする)。これは、$S(c+h)-S(c)$である。ここで、$c<t<c+h$なる$t$をとってきて、その点における$f(x)$の値$f(t)$を高さとする長方形の面積を考えることで、$t$を上手にとれば、$S(c+h)-S(c)=h\cdot f(t)$とできる。両辺を$h$で割り、$h\to 0$の極限を考えると、

$\underset{h\to 0}{\lim }\frac{S(c+h)-S(c)}{h}=\underset{h\to 0}{\lim }f(t)$

であるが、左辺は微分の定義より$S^{\prime }(c)$であり、$\underset{h\to 0}{\lim }t=c$であることに注意すると右辺は$f(c)$である。文字を$c$から$x$に取り換えると、結局

$S^{\prime }(x)=f(x)$

が得られる。つまり、$S(x)$は$f(x)$の原始関数の一つであることが分かる。

よって、$\underset{a}{\overset{b}{\int }}f(x)dx=S(b)-S(a)$であるが、この式の右辺は、関数$f(x)$のグラフと、直線$x=a$、直線$x=b$と、$x$軸で囲まれた面積である。よって、左辺$\underset{a}{\overset{b}{\int }}f(x)dx$は、関数$f(x)$のグラフと、直線$x=a$、直線$x=b$と、$x$軸で囲まれた面積を表している。

定積分と面積の関係

$a\le x\le b$　で、　$f(x)\ge 0$　のとき、直線 $x=a,x=b$ と $x$ 軸、 $f(x)$ で囲まれる面積 $S$ は $S=\underset{a}{\overset{b}{\int }}f(x)dx$

歴史的には、積分は、関数のグラフで囲まれた部分の面積を求めるために考え出された。この節で述べたような微分との関連は積分自体の発明よりずっと後になって発見されたことである。

例として、 $0\leqq x\leqq 1$の範囲で、y = xのグラフとx軸ではさまれた部分の面積を、積分を用いて計算する。 ( 実際にはこれは三角形なので、積分を用いなくても面積を計算することが出来る。 答は$\frac{1}{2}$ となる。 ) 定積分を行なうと、 $\underset{0}{\overset{1}{\int }}xdx$ $=\frac{1}{2}[x^2{]}_0^1$ $=\frac{1}{2}[1^2-0^2]$ $=\frac{1}{2}[1-0]$

$=\frac{1}{2}$ となり確かに一致する。

演習問題

放物線$y=5-x^2$とx軸および2直線$x=-1,x=2$で囲まれた部分の面積Sを求めよ。

解答

この放物線は$-1\le x\le 2$でx軸の上側にあるから、

$S=\underset{-1}{\overset{2}{\int }}(5-x^2)dx={[5x-\frac{x^3}{3}]}_{-1}^2=12$

$a\le x\le b$　において、常に　$f(x)\ge g(x)$　であるとき、2つの曲線　$y=f(x),y=g(x)$　に挟まれる部分の面積Sは、次の式で表される。

曲線 $y=f(x),y=g(x)$ の間の面積

$a\le x\le b$　で、　$f(x)\ge g(x)$　のとき、 $S=\underset{a}{\overset{b}{\int }}\{f(x)-g(x)\}dx$

• 問題例

• • 問題

放物線$y=x^2-1$と直線$y=x+1$によって囲まれた部分の面積Sを求めよ。

• • 解答

放物線と直線の交点のx座標は

$x^2-1=x+1$

$x^2-x-2=0$

$x=-1,x=2$

$-1\le x\le 2$の範囲で$x^2-1\le x+1$より

$S=\underset{-1}{\overset{2}{\int }}\{(x+1)-(x^2-1)\}dx=\underset{-1}{\overset{2}{\int }}(-x^2+x+2)dx={[-\frac{x^3}{3}+\frac{x^2}{2}+2x]}_{-1}^2=\frac{9}{2}$

$a\le x\le b$　で、　$f(x)\le 0$　のとき、x軸$y=0$と曲線$y=f(x)$によって挟まれていると考えられるので、

$S=\underset{a}{\overset{b}{\int }}\{0-f(x)\}dx=-\underset{a}{\overset{b}{\int }}f(x)dx$

となる。

面積(3)

$a\le x\le b$　で、　$f(x)\le 0$　のとき、 $S=-\underset{a}{\overset{b}{\int }}f(x)dx$

• 問題例

• • 問題

放物線$y=x^2-2x$とx軸で囲まれた部分の面積Sを求めよ。

• • 解答

放物線とx軸の交点のx座標は

$x^2-2x=0$

$x=0,x=2$

この放物線は$0\le x\le 2$でx軸の下側にあるから、

$S=-\underset{0}{\overset{2}{\int }}(x^2-2x)dx=-{[\frac{x^3}{3}-x^2]}_0^2=\frac{4}{3}$

本当にちょっとした余談

高校数学をしていると「将来微分とか積分とか何に使う？」と思う人の方が多いと思う。確かに日常生活では、積分などの高度な 数学は使わない。だがその一方裏では積分や 微分、高校数学では収まらないような数学が使われている。例えば台風の進路予想。 これは積分を使い台風の進路を予測している。他にもセキュリティの強化などにも数学は使われている。日常生活では数学は使わないが、数学に親しみを持ってみてはどうだろうか。

演習問題

(1)$F(x)=2x^2$のとき $f(x)$を求めよ。ただし$F^{\prime }(x)$

(2)$\underset{x\to c}{\lim }(x^2+x)=11$となる$c$を求めよ

(3)原始関数、定積分を求めよ

1)$\underset{3}{\overset{5}{\int }}\{2x^9+(6x-2x^3)\}dx$
2)$\int (\sin x+\tan x)dx$

3)$\underset{x\to 0}{\lim }\underset{x}{\overset{5}{\int }}2xdx$

4)$\underset{-60}{\overset{60}{\int }}(\sin x+{\cos }^{2}x)dx$

演習問題の解答とその手引き

(1)$f(x)=x^3$ 冪乗の微分は$y^{\prime }=n{x}^{n-1}$ であるため不定積分の定義より$f(x)=x^3$である。