中学数学3年 相似な図形

この章では、より進んだ平面図形の性質を扱います。特に、ある図形が相似の関係を持つときに、図形の間に成り立つ性質について述べます。

相似

相似な図形

たとえば、地図を見てみましょう。地図は、実際の地形と全く同じ形になるように書かれています。しかし、地図は持ち歩いたり、調査などに使うため、本物よりも小さく書かれています。例えば縮尺が25000分の1となっているなら、本物の25000分の1の大きさで、全く同じ形に書いてあるということになります。 また、本などを縮小コピーしたり、拡大コピーしてみましょう。やはり、原稿と同じように印刷されますが、大きさは変わっているはずです。

では、もっと簡単な図形である三角形はどうでしょうか。全く同じ形でも大きさが違う三角形では、どういう共通な性質を持っているでしょうか。

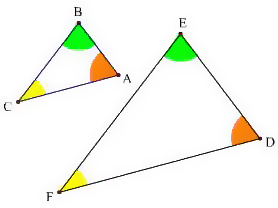
この2つの三角形は、全く同じ形をしていますが、大きさが違います。この2つの三角形を比べると、次のことが言えます。

• ∠A = ∠D、 ∠B = ∠E、 ∠C = ∠F
• AB:DE = BC:EF = CA:FD

ある2つの図形について、それらの図形の大きさだけが異なっていて、形は全く同じであるとき、この2つの図形は相似（そうじ）である、といいます。

相似な図形の性質

一般に、相似な図形では、次のことが成り立つ。 　対応する線分の長さの比はすべて等しい。 　対応する角の大きさはそれぞれ等しい。

また、円は半径に関わらず常に同じ形をしているので、すべて相似な図形であるといえます。 また、2年生で学習した合同な図形は、必ず相似の関係も満たしています。ただし、相似な図形は常に合同であるということは成り立ちません。

問題

次の図形が互いに相似であるかどうか述べよ。

1. 半径1cmの円と半径2cmの円
2. 辺の長さが2cm,3cm,4cmの三角形と4cm,6cm,8cmの三角形
3. 辺の長さが1cm,2cm,2cmの三角形と2cm,5cm,5cmの三角形
4. 辺の長さが3cm,4cm,5cmの三角形と別の3cm,4cm,5cmの三角形

解答

1. 円は半径に関わらず常に同じ形をしているので相似。
2. それぞれの辺の比が1:2の関係を満たしているので、それぞれの図形は相似。
3. それぞれの辺の比が等しくないので、これらの図形は相似ではない。
4. 2つの三角形は3辺が同じ長さを持っていることから互いに合同となっている。

合同な図形は相似な図形でもあるので、この2つの図形は相似となる。

相似比

相似な図形で、対応する線分の長さの比を相似比（そうじひ）といいます。

三角形の相似条件

2年生では三角形が合同になる条件を考えました。ここでは三角形が相似になる条件を考えてみましょう。

三角形の相似条件は、次のようになる。

三角形の相似条件

次の3つのうち、1つでも成り立てば相似である。 　3組の辺の比がすべて等しい。 　2組の辺の比とその間の角がそれぞれ等しい。 　2組の角がそれぞれ等しい。

相似の位置

相似の位置

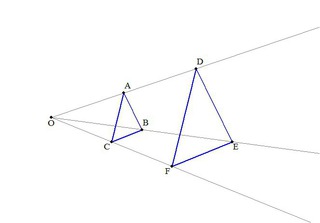
右の図は、$OD=2OA,OE=2OB,OF=2OC$となっている。 この図から次のことがわかる。

$OD:OA=OE:OB=OF:OC=2:1$

このように、2つの図形の対応する点を通る図形がすべて一点Oを通り、点Oからその点までの距離の比がすべて等しいとき、この2つの図形は相似の位置にあるといい、点Oを 相似の中心という。 この時、点Oから対応する点までの距離の比が2つの図形の相似比になる。

右の図の場合、相似比は1:2である。

平行線と相似

平行線と比

次に、上で得た相似の考えを用いて、一定の比を持つ平行線と交わる線分の間の 比について述べる。このとき、次の結果を得る。

ある一定の比を持つ間隔で並んでいる平行線を考えるとき、それらに任意の角度で交わる直線が作る線分は上で得た平行線間の間隔の比と等しい長さの比を持つ。

• 導出

平行線をそれぞれl,m,nと呼ぶ。 このとき、ある角度でl,m,nに交わる直線を取り、それらがl,m,nと交わる点を A,B,Cと呼ぶ。

• 図

ここで、Cからlに向かって下ろした垂線とlの交点をC'と呼び、 ここで、Bからlに向かって下ろした垂線とlの交点をB'と呼ぶ。 このとき、三角形ABB'とACC'は、互いに相似であることを示す。 実際、2つの三角形は直角三角形なので、どちらも90°の角を持っている。 更に、

$\mathrm{\angle }BA{B}^{\prime }=\mathrm{\angle }CA{C}^{\prime }$

は同じ角であるので同じ大きさである。よって、2つの角の大きさが等しいので、 上の2つの三角形は相似である。このことから、

$B{B}^{\prime }:C{C}^{\prime }=AB:AC$

が成り立つがこれは求めたかったことに等しい。

三角形と比

$\mathrm{△}ABC$の辺AB上に点Dをとり、$DE//BC$となるように辺AC上に点Eをとる。

$\mathrm{△}ABC$と$\mathrm{△}ADE$において、

共通な角だから、$\mathrm{\angle }BAC=\mathrm{\angle }DAE$

$DE//BC$から、$\mathrm{\angle }ABC=\mathrm{\angle }ADE$

2組の角がそれぞれ等しいから、$\mathrm{△}ABC$と$\mathrm{△}ADE$は相似である。

対応する辺の比が等しいから、$AD:AB=AE:AC=DE:BC$

上記に加えてさらに、$DF//AC$となるように辺BC上に点Fをとる。

$\mathrm{△}ADE$と$\mathrm{△}DBF$において、

$DE//BC$から、$\mathrm{\angle }ADE=\mathrm{\angle }DBF$

$DF//AC$から、$\mathrm{\angle }DAE=\mathrm{\angle }BDF$

2組の角がそれぞれ等しいから、$\mathrm{△}ADE$と$\mathrm{△}DBF$は相似である。

対応する辺の比が等しいから、$AD:DB=AE:DF$

また、四角形DFCEは2組の対辺がそれぞれ平行であるから平行四辺形である。

よって、$DF=EC$

$AD:DB=AE:DF$と$DF=EC$から、$AD:DB=AE:EC$

今までのことをまとめると次のようになる。

三角形と比(1)

$\mathrm{△}ABC$の辺AB、AC上にそれぞれ点D、Eをとるとき、次のようなことが成り立つ。 　$DE//BC$　ならば　$AD:AB=AE:AC=DE:BC$ 　$DE//BC$　ならば　$AD:DB=AE:EC$

この定理「三角形と比(1)」は逆も成り立つ。

1.の逆は「$\mathrm{△}ABC$の辺AB、AC上にそれぞれ点D、Eをとるとき、$AD:AB=AE:AC$　ならば　$DE//BC$」である。これを証明しよう。

$\mathrm{△}ADE$と$\mathrm{△}ABC$において、

仮定から、$AD:AB=AE:AC$

共通な角だから、$\mathrm{\angle }BAC=\mathrm{\angle }DAE$

2組の辺の比とその間の角が等しいから、$\mathrm{△}ADE$と$\mathrm{△}ABC$は相似である。

対応する角は等しいから、$\mathrm{\angle }ADE=\mathrm{\angle }ABC$

同位角が等しいから、$DE//BC$

一方、2.の逆は「$\mathrm{△}ABC$の辺AB、AC上にそれぞれ点D、Eをとるとき、$AD:DB=AE:EC$　ならば　$DE//BC$」である。これの証明は以下のようにできる。

$\mathrm{△}ADE$と$\mathrm{△}ABC$において、$AD:DB=AE:EC=a:b$とする。

$AD:AB=AD:(AD+DB)=a:(a+b)$

$AE:AC=AE:(AE+EC)=a:(a+b)$

よって$AD:AB=AE:AC$

共通な角だから、$\mathrm{\angle }BAC=\mathrm{\angle }DAE$

2組の辺の比とその間の角が等しいから、$\mathrm{△}ADE$と$\mathrm{△}ABC$は相似である。

対応する角は等しいから、$\mathrm{\angle }ADE=\mathrm{\angle }ABC$

同位角が等しいから、$DE//BC$

今までのことをまとめると次のようになる。

三角形と比(2)

$\mathrm{△}ABC$の辺AB、AC上にそれぞれ点D、Eをとるとき、次のようなことが成り立つ。 　$AD:AB=AE:AC$　ならば　$DE//BC$ 　$AD:DB=AE:EC$　ならば　$DE//BC$

中点連結定理

定理「三角形と比(2)」によると、「$\mathrm{△}ABC$の辺AB、AC上にそれぞれ点D、Eをとるとき、$AD:DB=AE:EC$　ならば　$DE//BC$」であった。

ここで、点D、Eをそれぞれ辺AB、ACの中点とすると、

$AD:DB=1:1$

だから、$DE//BC$がいえる。

また、$\mathrm{△}ADE$と$\mathrm{△}ABC$は相似であり、相似比は$1:2$となる。

$DE:BC=1:2$であるから、$2DE=BC$

よって

$DE=\frac{1}{2}BC$

今までのことをまとめると次のようになる。

中点連結定理

$\mathrm{△}ABC$の辺AB、AC上にそれぞれ中点D、Eをとるとき、次のようなことが成り立つ。 $DE//BC$　，　$DE=\frac{1}{2}BC$

このような定理を中点連結定理（ちゅうてん れんけつていり）という。

相似な図形の面積比と体積比

面積の比のことを面積比、体積の比のことを体積比（たいせきひ）という。

相似な平面図形の面積比

$\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$と$\mathrm{△}ABC$が相似であり、相似比が$k:1$のとき、$\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$の面積S'と$\mathrm{△}ABC$の面積Sの比を考える。

$BC=a$、BCに対する高さをhとすれば、$B^{\prime }{C}^{\prime }=ka$、B'C'に対する高さはkhとなるから

$S=\frac{1}{2}ah$

$S^{\prime }=\frac{1}{2}\times ka\times kh=k^2\times \frac{1}{2}ah=k^{2}S$

したがって

$S^{\prime }:S=k^{2}S:S=k^2:1$

相似な三角形の面積比は、相似比の2乗に等しい。

円Oと円O'が相似であり、相似比が$m:n$のとき、円Oの面積Sと円O'の面積S'の比を考える。

円Oの半径をmk、円O'の半径をnkとすると

$S=\pi \times (mk{)}^2=m^2\times k^2\pi$

$S^{\prime }=\pi \times (nk{)}^2=n^2\times k^2\pi$

したがって

$S:S^{\prime }=(m^2\times k^2\pi ):(n^2\times k^2\pi )=m^2:n^2$

今までのことをまとめると、次のようになる。

相似な平面図形の面積比

相似な平面図形の面積比は、相似比の2乗に等しい。 相似比が$m:n$ならば、面積比は$m^2:n^2$である。

角の二等分線に関する定理

※中高一貫校のみで扱う内容ですが、検定教科書でもわずかに触れられています。