高等学校数学C/数学的な表現の工夫

テンプレート:Pathnav 本項は高等学校数学Cの「数学的な表現の工夫」の解説です。

• 第1節「データの表現方法の工夫」では、身近な事象に関するデータを種類や目的に応じて表現する方法について学びます。
• 第2節「行列による表現とその演算」では、データの行列を用いた表し方と行列の基礎的な演算について学びます。
• 第3節「離散グラフによる表現」では、離散グラフを用いた表現方法と離散グラフを活用した問題解決について学びます。
• 第4節「行列の応用」では、前々課程数学C「行列とその応用」にて扱っていた発展内容と大学で学ぶ線形代数学のうち基礎的な内容を扱います。
• 第5節「コラム集」では、行列が身近な場面や今まで高校数学で扱ってきた分野に応用されている例を紹介します。

ベクトルの先行履修を推奨します。 複素数平面とはどちらの順番で履修しても構いません。

行列による表現とその演算

行列による表現

次の表は、ある月の第一週と第二週における、2つの店X, Yでの、3種類の色のボールペンの販売数を表したものである。

[第一週]

	黒	赤	青
X	55	64	20
Y	78	45	36

[第二週]

	黒	赤	青
X	50	44	16
Y	69	40	25

この表を、数字の並びを括弧で囲んだもので表すと、以下のようになる。

$A=\left(\begin{array}{ccc}55& 64& 20\\ 78& 45& 36\end{array}\right),B=\left(\begin{array}{ccc}50& 44& 16\\ 69& 40& 25\end{array}\right)$

上のように、いくつかの数や文字を長方形状に並べて両側を括弧で囲んだものを行列という。括弧の中のそれぞれの数や文字をその行列の成分という。行列は普通、大文字のアルファベットで表す。また、括弧は大括弧[]を用いても良い。

成分の横の並びを行、縦の並びを列という。行は上から、列は左から数える。m個の行とn個の列からなる行列をm行n列の行列（m×n行列）と呼ぶ。特に、行と列の個数が等しいn×n行列をn次の正方行列（あるいは単にn次行列）という。また、第i列と第j列の交わるところにある成分を(i, j)成分という。 例えば、上の行列Aの(1,2)成分は64である。

m×n行列$A$の(i, j)成分は普通、$a_{ij}$と表される。つまり、$A=\left(\begin{array}{cccccc}{a}_{11}& a_{12}& \cdots & a_{1j}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2j}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & \ddots & ⋮& ⋮\\ a_{i1}& a_{i2}& \cdots & a_{ij}& \cdots & a_{in}\\ ⋮& ⋮& \ddots & \ddots & ⋮& ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mj}& \cdots & a_{mn}\end{array}\right)$である。

ただ1行からなる行列を行ベクトル、ただ1列からなる行列を列ベクトルという。また、1や3+iのような定数は1×1行列と考えることができる。

2つの行列X, Yについて、行数と列数が共に等しいとき、「XとYは同じ型である」という。行列X, Yが同じ型且つ対応する成分がそれぞれ等しいとき、「XとYは等しい」といい、$X=Y$と書く。

• 例題

上の行列Aの第2行に現れる成分の和を求めよ。

• 解答

第2行にある成分は78, 45, 36であるため、$78+45+36=159$

• 例題

上の行列A, Bは同じ型であるかどうか答えよ。

• 解答

行列Aも行列Bも2×3行列であるため、同じ型である。

行列の和と差

同じ型である複数の行列については、四則演算を考えることができる。ここでは、2つの行列の和と差を考える。

同じ型の2つの行列X,Yの対応する成分の和を成分とする行列をXとYの和といい、$X+Y$と表す。同様に、同じ型の2つの行列X, Yの対応する成分の差を成分とする行列をXとYの差といい、$X-Y$と表す。

例えば、上の行列A, Bは同じ型であるから、その和と差はそれぞれ以下のようになる。

$A+B$

$=\left(\begin{array}{ccc}55& 64& 20\\ 78& 45& 36\end{array}\right)+\left(\begin{array}{ccc}50& 44& 16\\ 69& 40& 25\end{array}\right)$

$=\left(\begin{array}{ccc}55+50& 64+44& 20+16\\ 78+69& 45+40& 36+25\end{array}\right)$

$=\left(\begin{array}{ccc}105& 108& 36\\ 147& 85& 61\end{array}\right)$

$A-B$

$=\left(\begin{array}{ccc}55& 64& 20\\ 78& 45& 36\end{array}\right)-\left(\begin{array}{ccc}50& 44& 16\\ 69& 40& 25\end{array}\right)$

$=\left(\begin{array}{ccc}55-50& 64-44& 20-16\\ 78-69& 45-40& 36-25\end{array}\right)$

$=\left(\begin{array}{ccc}5& 20& 4\\ 9& 5& 11\end{array}\right)$

全成分が0である行列を零行列といい、型と無関係に$O$と表す。

行列の加法と減法について、以下の性質が成り立つ。

交換法則
 
$X+Y=Y+X$

結合法則

$(X+Y)+Z=X+(Y+Z)=X+Y+Z$

零行列と加減法

$X-X=O$, $X+O=X$

行列のスカラー倍

任意の定数kについて、行列Xの各成分のk倍を成分とする行列を$kX$で表す。

上の行列A, Bについて、その和$A+B$は第一週の販売数と第二週の販売数の合計を表すので、$\frac{1}{2}$倍した値は平均値となる。$P=A+B$とおくと、第一週の販売数と第二週の販売数の平均値は、

$\frac{1}{2}P$

$=\frac{1}{2}\left(\begin{array}{ccc}105& 108& 36\\ 147& 85& 61\end{array}\right)$

$=\left(\begin{array}{ccc}\frac{1}{2}\cdot 105& \frac{1}{2}\cdot 108& \frac{1}{2}\cdot 36\\ \frac{1}{2}\cdot 147& \frac{1}{2}\cdot 85& \frac{1}{2}\cdot 61\end{array}\right)$

$=\left(\begin{array}{ccc}52.5& 54& 18\\ 73.5& 42.5& 30.5\end{array}\right)$

となる。

行列$kA$に対して、$k=1$の時は$1\cdot X=X$, $k=0$の時は$0\cdot X=O$、$k=-1$の時は$-1\cdot X=-X$のように表す。また、aを正の数とするとき、$(-a)X=-(aX)$ より、これらを単に$-aX$のように書く。

行列のスカラー倍について、$k,l$を定数として以下の性質が成り立つ。

結合法則

$k(lA)=(kl)A=klA$

分配法則

$(k+l)A=kA+lA$, $k(A+B)=kA+kB$

$k,l$は実数に限らず、複素数でも良い。

行列の積

ここまでの内容を見返したとき、「似たような内容やったことあるな」と感じた人もいるだろう。 実は、ここまで見てきた行列の演算は、全てベクトルの成分演算を拡張したものになっている。

例えば、$\overrightarrow{a}=(1,3),\overrightarrow{b}=(2,5)$としたとき、

$\overrightarrow{a}+\overrightarrow{b}=(1,3)+(2,5)=(1+2,3+5)=(3,8)$

$\overrightarrow{a}-\overrightarrow{b}=(1,3)-(2,5)=(1-2,3-5)=(-1,-2)$

$3\overrightarrow{a}=3\cdot (1,3)=(3\cdot 1,3\cdot 3)=(3,9)$

である。

このとき、$\overrightarrow{a}=\left(\begin{array}{cc}1& 3\end{array}\right),\overrightarrow{b}=\left(\begin{array}{cc}2& 5\end{array}\right)$あるいは$\overrightarrow{a}=\left(\begin{array}{c}1\\ 3\end{array}\right),\overrightarrow{b}=\left(\begin{array}{c}2\\ 5\end{array}\right)$のように書き、行列とみなして計算しても同じ結果が得られる。

ここから、「行列はベクトルを拡張したもの」ということがわかる。

そこで、行列の積もベクトルの演算を拡張する形で定義しよう。 高校範囲において、数における掛け算に相当するベクトルの演算としてベクトルの内積があった。

内積を忘れてしまったという人向けに書いておくと、

2つの平面ベクトル$\overrightarrow{a}=(a_1,a_2),\overrightarrow{b}=(b_1,b_2)$の内積は$\overrightarrow{a}\cdot \overrightarrow{b}=a_1{b}_1+a_2{b}_2$

2つの空間ベクトル$\overrightarrow{a}=(a_1,a_2,a_3),\overrightarrow{b}=(b_1,b_2,b_3)$の内積は$\overrightarrow{a}\cdot \overrightarrow{b}=a_1{b}_1+a_2{b}_2+a_3{b}_3$

である。

ここで、$\overrightarrow{a}$をm次の列ベクトル、$\overrightarrow{b}$をm次の行ベクトルとみなし、$\overrightarrow{a}\cdot \overrightarrow{b}$と同じ結果になるように行ベクトルXと列ベクトルYの積XYを定義する。 すなわち、 $X=\left(\begin{array}{cccc}{x}_1& x_2& \cdots & x_m\end{array}\right),Y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right)$に対し、 $XY=\left(\begin{array}{cccc}{x}_1& x_2& \cdots & x_m\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right)=\sum _{k=1}^m{x}_k{y}_k$と定義する。

次は、これを元に一般の行列の積を考える。 行列Aの列数と行列Bの行数が等しいとき、Aの各行の成分の個数とBの各列の成分の個数が一致するから、積ABを考えることができる。

例えば、3つの列ベクトルP, Q, Rを並べた行列$\left(\begin{array}{ccc}P& Q& R\end{array}\right)$をSとおく。 このとき、行ベクトルAと行列Sの積は$AS=\left(\begin{array}{ccc}AP& AQ& AR\end{array}\right)$である。 同様に、3つの行ベクトルK, L, Mを並べた行列$\left(\begin{array}{c}K\\ L\\ M\end{array}\right)$をNとおくと、列ベクトルBと行列Nの積は$\left(\begin{array}{c}BK\\ BL\\ BM\end{array}\right)$である。

この2つから考えて、Aがl×m行列、Bがm×n行列のとき、積ABを、Aの第i行を取り出した行ベクトルとBの第j列を取り出した列ベクトルの積を(i, j)成分としたl×n行列と定める。

• 例題
  • 以下を計算せよ
    1. $\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{cc}x& z\\ y& w\end{array}\right)$
    2. $\left(\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right)\left(\begin{array}{cc}p& s\\ q& t\\ r& u\end{array}\right)$
  • 解答
    1. $\left(\begin{array}{cc}ax+by& az+bw\\ cx+dy& cz+dw\end{array}\right)$
    2. $\left(\begin{array}{cc}ap+bq+cr& as+bt+cu\\ dp+eq+fr& ds+et+fu\\ gp+hq+ir& gs+ht+iu\end{array}\right)$

なお、上とは別の方法で定義された行列の積もある。そちらの計算結果はこちらとは大幅に異なる。詳しくは「w:行列の乗法」を参照。

行列の乗法について、kを実数として以下の性質が成り立つ。

結合法則

$(kA)B=A(kB)=k(AB)=kAB$, $A(BC)=A(BC)=ABC$

分配法則

$(A+B)C=AC+BC$, $A(B+C)=AB+AC$

なお、結合法則の式において、$AB=a$あるいは$BC=a$となる場合、このaは1次行列であることに注意（行列の演算結果として出てきた一次行列を普通の定数とみなしてスカラー倍計算することはできない）。

• 例題
  • $A=\left(\begin{array}{cc}1& 1\\ 0& 2\end{array}\right)$, $B=\left(\begin{array}{cc}1& 2\\ 3& 0\end{array}\right)$, $C=\left(\begin{array}{cc}5& 2\\ 0& 7\end{array}\right)$について、以下を計算せよ。
    1. AB
    2. BA
    3. AC
    4. CA
  • 解答
    1. $AB=\left(\begin{array}{cc}4& 2\\ 6& 0\end{array}\right)$
    2. $BA=\left(\begin{array}{cc}1& 5\\ 3& 3\end{array}\right)$
    3. $AC=\left(\begin{array}{cc}5& 9\\ 0& 14\end{array}\right)$
    4. $CA=\left(\begin{array}{cc}5& 9\\ 0& 14\end{array}\right)$

上の例題からわかるように、行列の乗法では交換法則は一般には成り立たない

交換法則が成り立つ、すなわち$AB=BA$であるとき、「AとBは交換可能（可換）である」という。

なお、上の例題においては$(A+B)(A-B)\ne A^2-B^2$、$(A+C)(A-C)=A^2-C^2$である。 時間があったら確かめてみよう。

先ほど、「Aがl×m行列、Bがm×n行列のとき、積ABはAの第i行を取り出した行ベクトルとBの第j列を取り出した列ベクトルの積を(i, j)成分としたl×n行列」と定めたが、lとnが一致しない場合は$BA$が計算できない。一般に、AとBが同じ次数の正方行列ならば$AB,BA$ともに計算できる。

次の表は、太郎君の家で4月から7月までにスーパーで買った、飲食料品と他の商品の税込価格の合計である。

	飲食料品費	他商品費
4月	74520	15400
5月	68040	12100
6月	75600	13200
7月	69120	14300

消費税が飲食料品に8%、他の商品に10%掛かっているとして、この表から税額を計算したい。 この表を行列で表記すると$A=\left(\begin{array}{cc}74520& 15400\\ 68040& 12100\\ 75600& 13200\\ 69120& 14300\end{array}\right)$であり、第一列と第二列にそれぞれ$\frac{0.08}{1.08},\frac{0.1}{1.1}$を掛けられるような行列を考える。そのような行列を$P=\left(\begin{array}{cc}\frac{0.08}{1.08}& 0\\ 0& \frac{0.1}{1.1}\end{array}\right)$とおくと、$AP=\left(\begin{array}{cc}5520& 1400\\ 5040& 1100\\ 5600& 1200\\ 5120& 1300\end{array}\right)$である。第一列、第二列の成分を見ると、条件を満たしていることがわかる。

一般に、行列の左上の成分と右下の成分を結んだ対角線を主対角線といい、主対角線上の成分を対角成分という。対角成分以外の成分が全て0である正方行列を対角行列という。列ごとに定数倍したい場合、対角行列を掛ければ良い。

k番目の対角成分が$d_k$であるn次対角行列を$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(d_1,d_2,\cdots ,d_n)$と表す。

n次の対角行列において、対角成分が全て1であるものをn次の単位行列と呼び、$E$または$I_n$で表す。 例えば、２次の単位行列は$E=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$である。 n次の正方行列をAとすると、n次の単位行列$E$, n次の零行列$O$との間には次のような関係がある。

$AE=EA=A$
$AO=OA=O$

これは、実数における1、0の掛け算と同様の性質である。

なお、Aが対角行列であるとき、対角成分の和を跡（トレース）と言い$\mathrm{t}\mathrm{r}A$と表す。

• 例題
  • $A=\left(\begin{array}{cc}2& 1\\ 4& 2\end{array}\right)$, $B=\left(\begin{array}{cc}1& -2\\ -2& 4\end{array}\right)$の積ABを計算せよ
• 解答
  • $AB=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)=O$

上の例題のように、実数とは異なり$A\ne O$かつ$B\ne O$であっても$AB=O$となる場合がある。このとき、$A,B$を零因子という。

逆行列

0以外の実数において掛けたら1になるような数、逆数を考えたのと同様に、正方行列$X$に対し、掛けたら同じ型の単位行列$E$になるような行列を考える。この行列を逆行列といい、$X^{-1}$と表す。

正方行列$X$の逆行列$X^{-1}$が存在するならば、$X^{-1}$はただ一つに定まり、$X{X}^{-1}=X^{-1}X=E$を満たす。

2つの実数の商を「割られる数$a$と割る数$b$の逆数の積$\frac{a}{b}(=a{b}^{-1})$」で定義したように、2つの行列の商を「割られる行列$A$と割る行列$B$の逆行列の積$A{B}^{-1}$」と定義することができる。注意しなければならないのは、行列の積は先述の通り一般には可換でないので、実数のように分数表記を用いることはできない。

単位行列の逆行列を考える。単位行列の逆行列を$I$とおくと、逆行列の定義から$EI=IE=E$であり、単位行列の性質から$EI=IE=I$であることから$I=E$が成り立つ。すなわち、単位行列の逆行列はその単位行列自身である。

次に、零行列の逆行列を考える。逆行列の定義は「元の行列と掛けたら単位行列になる行列」であり、零行列は他の行列との積が必ず零行列になるため、零行列の逆行列は存在しない。

これらは実数における「1の逆数は1自身」「0の逆数は存在しない」という性質と同様である。

2次行列の逆行列について考える。

$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$に対し$P=\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$とすると、$AP=\left(\begin{array}{cc}ad-bc& 0\\ 0& ad-bc\end{array}\right)=(ad-bc)E$であり、$A(\frac{1}{ad-bc}P)=E$が成り立つ。すなわち、逆行列の定義より$A^{-1}=\frac{1}{ad-bc}P=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$である。

ただし、$ad-bc=0$の場合、$A$は逆行列$A^{-1}$を持たない。

正方行列Xに逆行列が存在するなら「Xは正則である」といい、存在しないなら「Xは特異である」という。逆行列が存在する正方行列を正則行列、存在しない正方行列を特異行列という。

• 問題
  • 零因子が特異行列であることを証明せよ。

2つの正則行列$A,B$について、$(AB{)}^{-1}=B^{-1}{A}^{-1}$が成り立つ。 これは、$AB(B^{-1}{A}^{-1})$と$(B^{-1}{A}^{-1})AB$の計算結果がともに$E$となることから明らかである。

次数が3以上の場合、逆行列の計算には次のガウスの消去法（掃き出し法）が用いられる。

ガウスの消去法（掃き出し法）I

正方行列Aの横に同じ次数の単位行列Eを並べた行列$\left(\begin{array}{cc}A& E\end{array}\right)$に行基本変形を施して$\left(\begin{array}{cc}E& B\end{array}\right)$となる場合、$B=A^{-1}$である。

行列を横に並べる際、2つの行列の区別のため境目に縦線｜を入れる場合がある。

行基本変形とは、次の3つの操作のことである。

1. ある行をc（≠0）倍する
2. 二つの行を交換する
3. ある行にある行のc（≠0）倍を加える

上の3つの操作は、それぞれ次の行列を右から掛けることと同値である。

1. n次単位行列$I_n$の(i, j)成分をcに置き換えた行列$P_n(i;c)$（ただし$c\ne 0$）
2. $I_n$の(i, i)成分と(j, j)成分を0に置き換え、(i, j)成分と(j, i)成分を1に置き換えた行列$P_n(i,j)$（ただし$i\ne j$）
3. $I_n$の(i, j)成分をcに置き換えた行列$P_n(i,j;c)$（ただし$i\ne j$）

この3つの行列を基本行列という。

なお、基本行列を左から掛けると列に対する操作になり、これを列基本変形という。行基本変形と列基本変形を纏めて「行列の基本変形」と呼ぶ。基本変形は可逆な操作であり、Aに基本変形を施してBになるならば、必ずBに基本変形を施してAに戻すことができる。

• 例題
  • $P=\left(\begin{array}{ccc}1& 1& -1\\ -2& 0& 1\\ 0& 2& 1\end{array}\right)$の逆行列を求めよ。
• 解答

Pと3次単位行列Eを並べた行列は

$\left(\begin{array}{cccccc}1& 1& -1& 1& 0& 0\\ -2& 0& 1& 0& 1& 0\\ 0& 2& 1& 0& 0& 1\end{array}\right)$

である。

一行目の2倍を二行目に加えて

$\left(\begin{array}{cccccc}1& 1& -1& 1& 0& 0\\ 0& 2& -1& 2& 1& 0\\ 0& 2& 1& 0& 0& 1\end{array}\right)$

二行目の1/2倍を一行目から引き、三行目から二行目を引いて

$\left(\begin{array}{cccccc}1& 0& -\frac{1}{2}& 0& -\frac{1}{2}& 0\\ 0& 2& -1& 2& 1& 0\\ 0& 0& 2& -2& -1& 1\end{array}\right)$

三行目の1/4倍を一行目に加え、三行目の1/2倍を二行目に加えて

$\left(\begin{array}{cccccc}1& 0& 0& -\frac{1}{2}& -\frac{3}{4}& \frac{1}{4}\\ 0& 2& 0& 1& \frac{1}{2}& \frac{1}{2}\\ 0& 0& 2& -2& -1& 1\end{array}\right)$

二行目と三行目を1/2倍して

$\left(\begin{array}{cccccc}1& 0& 0& -\frac{1}{2}& -\frac{3}{4}& \frac{1}{4}\\ 0& 1& 0& \frac{1}{2}& \frac{1}{4}& \frac{1}{4}\\ 0& 0& 1& -1& -\frac{1}{2}& \frac{1}{2}\end{array}\right)$

線で区切った左側の行列がEになっているので、求める逆行列は線で区切った右側の行列、すなわち$\left(\begin{array}{ccc}-\frac{1}{2}& -\frac{3}{4}& \frac{1}{4}\\ \frac{1}{2}& \frac{1}{4}& \frac{1}{4}\\ -1& -\frac{1}{2}& \frac{1}{2}\end{array}\right)$である。

発展：転置と表操作

行列$A$に対し、その列と行を入れ替えた行列を$A$の転置行列といい、${}^{t}A$と表す。$A$から${}^{t}A$を作ることを、「Aを転置する（Aの転置をとる）」という。

例えば、$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$に対し、${}^{t}A=\left(\begin{array}{cc}a& c\\ b& d\end{array}\right)$である。

また、列ベクトルの転置は行ベクトルとなる。

その定義より、${}^t({}^{t}A)=A$である。

X, Yを同じ型の行列、kを定数とすると${}^t(X+Y)={}^{t}X+{}^{t}Y,{}^t(kX)=k{}^{t}X$が成り立つ。

また、行列$A,B$とその転置行列${}^{t}A,{}^{t}B$について、${}^t(AB)={}^{t}B{}^{t}A$が成り立つ。

${}^{t}A=A$を満たす行列を対称行列、${}^{t}A=-A$を満たす行列を交代行列という。

例えば、対角行列は対称行列である。

対称行列かつ交代行列である行列は$O$のみである。

また、任意の正方行列$A$に対し、$A=\frac{A+{}^{t}A}{2}+\frac{A-{}^{t}A}{2}$が成り立つ。このとき、$\frac{A+{}^{t}A}{2}$は対称行列、$\frac{A-{}^{t}A}{2}$は交代行列であることが、それぞれの転置をとることで確認できる。

正則行列Aに関して、$({}^{t}A{)}^{-1}={}^t(A^{-1})$が成り立つ。

この節の最初に「行列は数や文字を長方形状に並べたもの」と述べたが、行列の積を考えるときに「行列は数ベクトルを1方向に並べたもの」という考え方を使った。 この考え方を用いると、以下が成り立つことがわかる。

$a_1,a_2,\cdots ,a_n$を同じ型の列ベクトルとすると、$A=\left(\begin{array}{cccc}{a}_1& a_2& \cdots & a_n\end{array}\right)$について${}^{t}A=\left(\begin{array}{c}{}^t{a}_1\\ {}^t{a}_2\\ ⋮\\ {}^t{a}_n\end{array}\right)$である。

行列$A$がm×n行列であるとき、その転置行列${}^{t}A$はn×m行列である。そのため、$A{}^{t}A$と${}^{t}AA$は常に計算可能である。また、計算結果は対称行列となる。

$A{}^{t}A={}^{t}AA=E$となる正方行列Aを考える。このような行列を直交行列という。

一般に直交行列は正則行列であり、${}^{t}A=A^{-1}$が成り立つ。直交行列の逆行列は直交行列であり、上式から直交行列の転置行列も直交行列である。2つの直交行列の積もまた直交行列になる。

次の表は、3人の中学生Aさん, Bさん, Cさんの定期テストの点数を表した表である。

	国語	数学	英語	理科	社会
A	65	82	78	96	67
B	85	63	90	65	94
C	98	76	70	85	90

この表を行列で表すと、$P=\left(\begin{array}{ccccc}65& 82& 78& 96& 67\\ 85& 63& 90& 65& 94\\ 98& 76& 70& 85& 90\end{array}\right)$である。

この行列から一部の行や列のみを取り出すことを考える。

例えば国語の点数（一列目）のみを取り出したい場合、$\left(\begin{array}{c}1\\ 0\\ 0\\ 0\\ 0\end{array}\right)$という行列を右から掛ければ良い。実際に計算すると、$P\left(\begin{array}{c}1\\ 0\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}65\\ 85\\ 98\end{array}\right)$である。

ここで、一つの成分が1で残りの成分が0である列ベクトルを基本ベクトルといい、1である場所が上からi番目であるとき、$e_i$と表す。例えば、上の計算で用いた5次列ベクトルは$e_1$である。なお、この記号は列ベクトルの型によらず用いるため、常に型に注意する必要がある。

複数列を抽出する場合、取り出したい列を$a,b,\cdots$ とすると、Pに行列$\left(\begin{array}{ccc}{e}_a& e_b& \cdots \end{array}\right)$を右からかければ良い。

また、複数列の抽出を応用することにより、表の列を並べ替えることができる。

例えば、上の表の点数を「英語, 数学, 国語 , 社会, 理科」の順に並べ替えたい場合、$P\left(\begin{array}{ccccc}{e}_3& e_2& e_1& e_5& e_4\end{array}\right)$を計算すれば良い。

行に対して操作する場合、基本ベクトルを転置して左から掛ければ良い。

例えば、Cさんの点数を抽出する場合、${}^t{e}_{2}P=\left(\begin{array}{ccc}0& 1& 0\end{array}\right)\left(\begin{array}{ccccc}65& 82& 78& 96& 67\\ 85& 63& 90& 65& 94\\ 98& 76& 70& 85& 90\end{array}\right)=\left(\begin{array}{ccccc}98& 76& 70& 85& 90\end{array}\right)$と計算する。

複数行の抽出や行の並べ替えも同様にできる。

例えば、「Cさん, Aさん, Bさん」の順番で並べる場合、$\left(\begin{array}{c}{}^t{e}_3\\ {}^t{e}_1\\ {}^t{e}_2\end{array}\right)P$を計算すれば良い。

列操作と行操作を同時に行うことで、特定の成分を取り出すこともできる。

一般に、各行各列に1が一つづつ配置され、残りの成分が全て0である行列を置換行列という。例えば、単位行列は置換行列である。置換行列は直交行列でもある。

次に、各行・各列の和を求めることを考える。

行列の積を考えたとき、先に列ベクトルと行ベクトルの積を考えた。その考え方を用いると、各列の和を求めたい場合、元の行列に成分が全て1である列ベクトルを右から掛ければ良い。

ここでは、全ての成分が1であるn次列ベクトルを$J_n$と表すこととする。

例えば、上の表で3人の点数の合計を計算すると、$P{J}_5=\left(\begin{array}{ccccc}65& 82& 78& 96& 67\\ 85& 63& 90& 65& 94\\ 98& 76& 70& 85& 90\end{array}\right)\left(\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\right)=\left(\begin{array}{ccc}388& 397& 419\end{array}\right)$である。

各行の和を求める場合、${}^t{J}_n$を左からかければ良い。

また、掛ける数ベクトルの成分の値を変えることにより、目的に応じてさまざまな合計を出すことができる。

ここまで行列の積・転置操作の応用として表操作を見てきたが、もう一つ応用を考えよう。

2つのベクトル$\overrightarrow{OP},\overrightarrow{OQ}$の成分を列ベクトルを用いて$\overrightarrow{OP}=\left(\begin{array}{c}a\\ b\end{array}\right),\overrightarrow{OQ}=\left(\begin{array}{c}c\\ d\end{array}\right)$と表す。 このとき、$|\overrightarrow{OP}{|}^2=a^2+b^2,|\overrightarrow{OQ}{|}^2=c^2+d^2,\overrightarrow{OP}\cdot \overrightarrow{OQ}=ac+bd$である。

$A=\left(\begin{array}{cc}\overrightarrow{OP}& \overrightarrow{OQ}\end{array}\right)$とおくと、 ${}^{t}AA=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{cc}a& c\\ b& d\end{array}\right)=\left(\begin{array}{cc}{a}^2+b^2& ac+bd\\ ac+bd& c^2+d^2\end{array}\right)=\left(\begin{array}{cc}|\overrightarrow{OP}{|}^2& \overrightarrow{OP}\cdot \overrightarrow{OQ}\\ \overrightarrow{OP}\cdot \overrightarrow{OQ}& |\overrightarrow{OQ}{|}^2\end{array}\right)$となる。

特に$|\overrightarrow{OP}|=|\overrightarrow{OQ}|=1$のとき、${}^{t}AA=\left(\begin{array}{cc}1& \cos \theta \\ \cos \theta & 1\end{array}\right)$である（ただし、$\theta$は$\overrightarrow{OP}$と$\overrightarrow{OQ}$の成す角）。

このようにして、ベクトルの成す角$\theta$を求めることができる。

ここまで行列のさまざまな演算を見てきたが、普通の数と同様に演算順が決まっている。 具体的には、

1. 括弧の中の計算
2. 逆行列・転置をとる計算
3. スカラー倍・積の計算
4. 和・差の計算

を式の左側から順に行っていく。

離散グラフによる表現

離散グラフ

点とそれらを結ぶ線で構成された図を離散グラフという。離散グラフの点を頂点、線を辺、頂点に集まる辺の本数をその頂点の次数という。 ここでは辺の向きは考えない（無向グラフのみを扱う）。

グラフ$G$を構成する頂点の集合を$V$、辺の集合を$E$とし、$G=(V,E)$と表記する。頂点を$u$や$v$で表すことが多く、頂点$u,v$を結ぶ辺を$\{u,v\}$と表記する。

• 例題
  • グラフ$G=(\{v_1,v_2,v_3,v_4\},\{\{v_1,v_2\},\{v_1,v_3\},\{v_1,v_4\},\{v_2,v_3\},\{v_3,v_4\}\})$を作図せよ。
  • 解答

• 
  $G$

一筆書き

以下、「ケーニヒスベルクの橋の問題」を例に、離散グラフの一筆書きについて考える。

ブレーゲル川と七つの橋を示したオイラーの時代のケーニヒスベルク

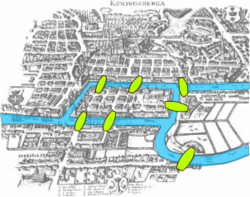
18世紀の初め頃、東プロイセンの首都であるケーニヒスベルク （現・ロシア、カリーニングラード）という大きな町があった。この町の中央には、プレーゲル川という大きな川が流れており、七つの橋が架けられていた。あるとき町の人が、次のように言った。

「このプレーゲル川に架かっている7つの橋を2度通らずに、全て渡って、元の所に帰ってくることができるか。ただし、どこから出発してもよい」

町の人が言ったことはできるだろうか。

1736年、レオンハルト・オイラーは、この問題を以下の離散グラフに置き換えて考えた。

→

このグラフが一筆書き可能であれば、ケーニヒスベルクの橋を全て1度ずつ通って元の場所に戻ってくるルートが存在することになる。

離散グラフのどの2頂点も幾つかの辺を辿って一方から他方へ行けるとき、その離散グラフは「連結である」という。

ここでは、次数が奇数である頂点を奇点、次数が偶数である頂点を偶点、一筆書きの始める頂点を始点、一筆書きを終える頂点を終点、そのどちらでもない頂点を途中点と呼ぶことにする。

途中点ではその頂点に集まる辺を使って「入る」「出る」が繰り返され、最後は必ず「出る」で終わる。つまり、途中点は必ず偶点になる。 奇点が始点である場合、終点では「入る」「出る」が繰り返され、最後は「入る」でおわる。つまり、奇点が始点であるならば、終点もまた奇点である。

したがって、一筆書きができる離散グラフに奇点があれば、奇点は2つあり、それらは必ず始点・終点のペアになる。すなわち、離散グラフにおいて、奇点の個数が1または3以上であるならば一筆書きはできない。

このことを言い換えたのが、次のオイラーグラフの定理である。

オイラーグラフの定理

連結である離散グラフにおいて一筆書きができるための必要十分条件は、奇点の個数が0または2であることである。

奇点の数が0であるとき、離散グラフには偶点しか存在せず、どの偶点を始点にしても必ず元の点に戻ってくる。このように、一筆書きが可能でどの点から始めても始点と終点が一致する離散グラフをオイラーグラフという。

経路の数え上げ

行列の冪乗についても指数法則が成り立つ。

離散グラフの応用

多面体と離散グラフ

場合の数と離散グラフ

発展：行列の応用

行列式・固有値

二次行列$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$に対し$A^{-1}$が存在する必要十分条件は$ad-bc\ne 0$であった。つまり、$ad-bc$という式はAの判別式のような役割をする。 この式を二次行列の行列式といい、$|A|$もしくは$\mathrm{d}\mathrm{e}\mathrm{t}A$と表す。行列の成分を表示して記す場合、行列の括弧を外して絶対値記号の中に成分を並べ$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$のように表すか、括弧の左にdetを書いて$\mathrm{d}\mathrm{e}\mathrm{t}\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$と表す。絶対値記号を用いてはいるが、行列式は負の値をとり得るので注意。

3次行列$\left(\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right)$の行列式は$\left|\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right|=aei-afh+bfg-bdi+cdh-ceg$である。

一般に、n次行列の行列式の値は$n!$個の項の足し算/引き算で求まり、各項は$n$個の成分の積となっている。

行列式の正式な定義は省略するが、実用上、4次以上の行列式を定義通りに計算することはほとんどない。また、行列式は正方行列にしか定義されない。

$|(\mathrm{d}\mathrm{e}\mathrm{t}A)|$はAを構成する列ベクトルの張る図形の体積であることが知られている。例えば、3次行列の場合、行列式の値の絶対値は各列ベクトルの張る平行六面体の体積と一致する。

次の公式が成り立つ。 $\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ & a_{22}& \cdots & a_{2n}\\ & & \ddots & ⋮\\ \mathrm{O}& & & a_{nn}\end{array}\right|=\left|\begin{array}{cccc}{a}_{11}& & & \mathrm{O}\\ a_{21}& a_{22}& & \\ ⋮& ⋮& \ddots & \\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|=\prod _{k=1}^n{a}_{kk}$

第一式の中身は上三角行列、第二式の中身は下三角行列と呼ばれる行列である。ただし、$\mathrm{O}$は0の集まりを表す。2つ合わせて三角行列という。第三式の$\prod _{k=1}^n$は「kに1からnまで代入したものを全て掛ける」という意味の記号（簡単に言えば$\sum _{k=1}^n$の掛け算バージョン）であり、$\mathrm{\Pi }$は$\pi$の大文字である。

n次行列Aからi行目とj列目を除いた行列を$A_{ij}$と表す。 このとき、$(-1{)}^{i+j}\times \mathrm{d}\mathrm{e}\mathrm{t}{A}_{ij}$を(i, j)余因子と呼び、${\mathrm{\Delta }}_{ij}$と表す。

正方行列Aに対し、(i, j)成分が${\mathrm{\Delta }}_{ij}$である行列の転置行列を余因子行列といい、$\tilde{A}$と表す。

Aが正則ならば、$A^{-1}=\frac{\tilde{A}}{\mathrm{d}\mathrm{e}\mathrm{t}A}$が成り立つが、これを利用して逆行列を求めるよりは、行基本変形で求めた方が遙かに計算量が少なくて済む。

余因子展開

正方行列$A$の行列式$\mathrm{d}\mathrm{e}\mathrm{t}A$について、$i$を任意の非負整数とすると$\mathrm{d}\mathrm{e}\mathrm{t}A=\sum _{j=i}^n{a}_{ij}{\mathrm{\Delta }}_{ij}$と展開できる。

実際に行列式を計算する場合、余因子展開を行う前に基本変形で一行目・一列目に0を増やすと計算しやすくなる。余因子展開を繰り返すことにより二次・三次または三角行列の行列式の四則演算に帰着でき、次数の大きい行列の行列式が簡単に計算できる。

対角行列の行列式は対角成分の総積となる。単位行列は成分が全て1である対角行列なので、その行列式は1である。零行列の行列式は0である。

正方行列$A$について、

$A$が正則$⟺\mathrm{d}\mathrm{e}\mathrm{t}A\ne 0⟺A$を構成する行/列ベクトル同士が一次独立

が成り立つ。

一般の正方行列について$\mathrm{d}\mathrm{e}\mathrm{t}({}^{t}A)=\mathrm{d}\mathrm{e}\mathrm{t}A$が成り立つ。また、正則行列について$\mathrm{d}\mathrm{e}\mathrm{t}(A^{-1})=(\mathrm{d}\mathrm{e}\mathrm{t}A{)}^{-1}=\frac{1}{\mathrm{d}\mathrm{e}\mathrm{t}A}$が成り立つ。

正方行列に対して基本変形を施すと、行列式は以下のように変化する。

1. 第i行/列のc倍を第j列/行に加える変形をしても、行列式の値は変わらない。
2. 第i行/列と第j行/列を入れ替える変形をすると、行列式の符号が逆転する。
3. 第j行/列を$c(\ne 0)$倍すると、行列式の値もc倍される。

行列の積について$\mathrm{d}\mathrm{e}\mathrm{t}(AB)=\mathrm{d}\mathrm{e}\mathrm{t}A\times \mathrm{d}\mathrm{e}\mathrm{t}B$が成り立つ。

• 問題
  • 行列式を用いて次の行列が正則行列であるかどうか判定せよ。
    1. $\left(\begin{array}{cc}3& 6\\ 2& 4\end{array}\right)$
    2. $\left(\begin{array}{ccc}1& -2& 4\\ 7& -3& 8\\ 5& -9& 6\end{array}\right)$
    3. $\left(\begin{array}{cccc}12& 4& 27& 31\\ -4& 18& -23& 41\\ 67& 9& -3& 7\\ -3& 4& 57& -11\end{array}\right)$

直交行列Aについて、$|(\mathrm{d}\mathrm{e}\mathrm{t}A)|=1$が成り立つ。

• 例題
  • 上記を証明せよ
• 解答

直交行列はその転置行列が逆行列に等しい行列なので、

$\mathrm{d}\mathrm{e}\mathrm{t}E=\mathrm{d}\mathrm{e}\mathrm{t}(A{A}^{-1})=\mathrm{d}\mathrm{e}\mathrm{t}(A{}^{t}A)=\mathrm{d}\mathrm{e}\mathrm{t}A\times \mathrm{d}\mathrm{e}\mathrm{t}({}^{t}A)=(\mathrm{d}\mathrm{e}\mathrm{t}A{)}^2$

ここで$\mathrm{d}\mathrm{e}\mathrm{t}E=1$なので、二次方程式$(\mathrm{d}\mathrm{e}\mathrm{t}A{)}^2=1$を解いて$|(\mathrm{d}\mathrm{e}\mathrm{t}A)|=1$となる。

ベクトルの外積は行列式を用いて表記できる。

$\overrightarrow{a}=\left(\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right),\overrightarrow{b}=\left(\begin{array}{c}{b}_x\\ b_y\\ b_z\end{array}\right)$、3つの座標軸の基本ベクトルをそれぞれ$\overrightarrow{e_x},\overrightarrow{e_y},\overrightarrow{e_z}$としたとき、$\overrightarrow{a}\times \overrightarrow{b}=\left(\begin{array}{c}{a}_y{b}_z-a_z{b}_y\\ a_z{b}_x-a_x{b}_z\\ a_x{b}_y-a_y{b}_x\end{array}\right)$を基本ベクトルの一次結合で表すと、

$(a_y{b}_z-a_z{b}_y)\overrightarrow{e_x}+(a_z{b}_x-a_x{b}_z)\overrightarrow{e_y}+(a_x{b}_y-a_y{b}_x)\overrightarrow{e_z}$

係数部分を行列式表記にすると、

$\left|\begin{array}{cc}{a}_y& a_z\\ b_y& b_z\end{array}\right|\overrightarrow{e_x}+\left|\begin{array}{cc}{a}_z& a_x\\ b_z& b_x\end{array}\right|\overrightarrow{e_y}+\left|\begin{array}{cc}{a}_x& a_y\\ b_x& b_y\end{array}\right|\overrightarrow{e_z}$

2つ目の行列式の各列を入れ替えると基本変形の性質より、

$\left|\begin{array}{cc}{a}_y& a_z\\ b_y& b_z\end{array}\right|\overrightarrow{e_x}-\left|\begin{array}{cc}{a}_x& a_z\\ b_x& b_z\end{array}\right|\overrightarrow{e_y}+\left|\begin{array}{cc}{a}_x& a_y\\ b_x& b_y\end{array}\right|\overrightarrow{e_z}$

3つの基本ベクトルを3次の行列式の一行目の成分と考えて余因子展開の逆を行なうと、

$\left|\begin{array}{ccc}\overrightarrow{e_x}& \overrightarrow{e_y}& \overrightarrow{e_z}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|$

よって、

$\overrightarrow{a}\times \overrightarrow{b}=\left|\begin{array}{ccc}\overrightarrow{e_x}& \overrightarrow{e_y}& \overrightarrow{e_z}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|$

この式を見ると、一行目は座標軸の基本ベクトル、二行目は$\overrightarrow{a}$の成分、三行目は$\overrightarrow{b}$の成分がx,y,zの順番で並んでいて整然としている。

ケーリー・ハミルトンの定理
 
二次行列$A$について、$A^2-(\mathrm{t}\mathrm{r}A)A+(\mathrm{d}\mathrm{e}\mathrm{t}A)E=O$が成り立つ。

これを用いて、$A^n$の次数下げを行うことができる。 具体的には、$A^n=A^{n-2}{A}^2=A^{n-4}{A}^2{A}^2\cdots$と変形し、$A^2=(\mathrm{t}\mathrm{r}A)A-(\mathrm{d}\mathrm{e}\mathrm{t}A)E$を順次代入していく。代入の過程で出た$A^2$にも順次代入すると、最終的には$A$の一次式となる。

• 例題
  • ケーリー・ハミルトンの定理を利用して「二次行列Aが特異行列である$⟺\mathrm{d}\mathrm{e}\mathrm{t}A\ne 0$」を証明せよ。

$M^n=O(M\ne O)$を満たす行列$M$を冪零行列という。

• 例題
  • 1. 冪零行列は逆行列を持たないことを証明せよ。
  • 2. ケーリー・ハミルトンの定理を利用して、「二次行列Aが冪零行列$⟹A^2=O$」を証明せよ。

行列式と同じように行列の特性を表す値がある。それが以下で扱う固有値である。固有値は量子力学やグラフ理論など、数多の場面で活躍する重要な概念である。

n次行列Aに対し、$A𝐱=\lambda 𝐱$を満たす 複素数$\lambda$をAの固有値、列ベクトル$𝐱$を固有値に対する固有ベクトルという。なお、$\lambda$はラムダと読むギリシャ文字である。また、固有ベクトルの長さは議論に関係ない。つまり、$𝐱$が固有ベクトルならば$k𝐱(k\ne 0)$も固有ベクトルである。普通、「固有ベクトルを求めよ」と聞かれたら　固有ベクトルのうち最も簡単なものを答える。

注意：$𝐚$は$\overrightarrow{a}$と同じ意味の記号である。ベクトルが常に有向線分を表すわけではないため、大学では矢印を付ける代わりに太文字を用いて表すことが多い。このページでは「$𝐚$：一般のベクトル、$\overrightarrow{a}$：有向線分を表すベクトル」と使い分ける。

$I_n$をn次単位行列とすると、

$A𝐱=\lambda 𝐱⟺\lambda 𝐱-A𝐱=O⟺(\lambda I_n-A)𝐱=O$

最後の式を考えると、$(\lambda I_n-A)𝐱=O$となる$𝐱(\ne O)$が存在する必要十分条件は$\lambda I_n-A$が特異行列であることである。

すなわち、

$\mathrm{d}\mathrm{e}\mathrm{t}(\lambda I_n-A)=0$

が成り立つ。

この方程式をAの固有方程式（特性方程式）という。

また、左辺の行列式はn次の多項式に展開できる。この多項式をAの固有多項式と言い、${\mathrm{\Phi }}_A(\lambda )$と表す。ただし、$\mathrm{\Phi }$はファイと読むギリシャ文字である。

固有方程式の解を考えると、n次正方行列$A$の固有値は値の重複を含めてn個(${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$)あることがわかる。逆に、固有多項式は${\mathrm{\Phi }}_A(\lambda )=\prod _{i=1}^n(\lambda -{\lambda }_i)$と表せる。固有値の値の重複を考慮に入れて書き換えると、$r\leqq n$として${\mathrm{\Phi }}_A(\lambda )=\prod _{i=1}^r(\lambda -{\lambda }_i{)}^{{\nu }_i}$となる。このとき、${\nu }_i$を${\lambda }_i$に対する（代数学的）重複度という。なお、$\nu$はニューと読むギリシャ文字である。

固有方程式の$\lambda$を強引に$A$へ置き換えると、n次行列についてのケーリー・ハミルトンの定理が得られる。（$A$は行列、$\lambda$は定数なので、「固有方程式${\mathrm{\Phi }}_A(\lambda )=O$に$A$を代入すれば明らか」という証明はできない。）

固有値を正しく計算できているか確かめる方法として、次の性質が用いられる。

正方行列Aについて、$\mathrm{t}\mathrm{r}A=\sum _{i=1}^n{\lambda }_i$

• 例題

$\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)$の固有値と対応する固有ベクトルをそれぞれ求めよ。

• 解答

固有方程式に代入すると、

$\mathrm{d}\mathrm{e}\mathrm{t}(\lambda \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)-\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right))=0$

整理すると

$\mathrm{d}\mathrm{e}\mathrm{t}\left(\begin{array}{cc}\lambda -4& -1\\ 2& \lambda -1\end{array}\right)=0$

計算して

$(\lambda -4)(\lambda -1)-(-1)\times 2=0$

${\lambda }^2-5\lambda +6=0$

$(\lambda -2)(\lambda -3)=0$

$\therefore \lambda =2,3$

ここで元の行列の跡は5、求めた固有値の和は5なので、正しく求められていることが確かめられた。

固有値2に対応する固有ベクトルは、

$\left(\begin{array}{cc}2-4& -1\\ 2& 2-1\end{array}\right)X=O$より

$X=\left(\begin{array}{c}1\\ -2\end{array}\right)$と求まる。

固有値3に対応する固有ベクトルは、

$\left(\begin{array}{cc}3-4& -1\\ 2& 3-1\end{array}\right)X=O$より

$X=\left(\begin{array}{c}1\\ -1\end{array}\right)$と求まる。

• 問題

$\left(\begin{array}{ccc}2& 1& -1\\ -4& -3& -1\\ 4& 4& 2\end{array}\right)$の固有値を求めよ。

転置行列について${\mathrm{\Phi }}_A(\lambda )={\mathrm{\Phi }}_{{}^{t}A}(\lambda )$が成り立つ。

固有多項式に$\lambda =0$を代入すると以下の定理が得られる。

Aをn次行列、その固有値を${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$とすると、$\mathrm{d}\mathrm{e}\mathrm{t}A=\prod _{i=1}^n{\lambda }_i$

このことから、0は正則行列の固有値になり得ないことがわかる。 そこで、逆行列の固有値について考える。

正則行列Aの固有ベクトルを${𝐱}_{\lambda }$とおく。

固有値の定義から、

$A{𝐱}_{\lambda }=\lambda {𝐱}_{\lambda }$

Aの逆行列を両辺に左から掛けて、

$E{𝐱}_{\lambda }=\lambda A^{-1}{𝐱}_{\lambda }$

$\lambda \ne 0$なので、

$\frac{1}{\lambda }{𝐱}_{\lambda }=A^{-1}{𝐱}_{\lambda }$

よって、$A^{-1}$の固有値は$\frac{1}{\lambda }$

つまり、逆行列の固有値は元の行列の固有値の逆数であり、固有ベクトルは元の行列と共通である。

固有値は複素数であるため、複素数平面上に描画できる。 特殊な行列の固有値について紹介すると、

• 対称行列の固有値は全て実軸上に存在する
• 交代行列の固有値は全て虚軸上に存在する
• 直交行列の固有値は全て単位円上に存在する

正方行列$A,B$に対して$B=P^{-1}AP$となる正則行列$P$が存在するならば、「$A,B$は相似である」といい、$A\sim B$と表す。$A$を$P^{-1}$と$P$で挾む操作を相似変換という。

行列の相似について、以下が成立する。

• $A\sim A$
• $A\sim B⟹B\sim A$
• $A\sim B\wedge B\sim C⟹A\sim C$

($A\wedge B$は「A且つB」を意味する論理記号である。)

相似な行列A, Bについて、以下が成り立つ。

• $\mathrm{d}\mathrm{e}\mathrm{t}A=\mathrm{d}\mathrm{e}\mathrm{t}B$
• $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}B$
• ${\lambda }_A={\lambda }_B$
• $\mathrm{t}\mathrm{r}A=\mathrm{t}\mathrm{r}B$
• $A^n\sim B^n$

上の5つの性質は簡単に証明できるので、時間があれば挑戦してみよう。

正方行列$A$を相似変換によって対角行列$D$に変換することを行列の対角化という。

行列が対角化可能である必要十分条件を求める。

$P^{-1}AP=D$の$D$を成分表示すると、

$P^{-1}AP=\left(\begin{array}{cccc}{d}_1& 0& \cdots & 0\\ 0& d_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & d_n\end{array}\right)$

両辺にPを左から掛けて

$AP=P\left(\begin{array}{cccc}{d}_1& 0& \cdots & 0\\ 0& d_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & d_n\end{array}\right)$

ここで$P$を列ベクトル${𝐱}_i$を用いて表すと$P=\left(\begin{array}{cccccc}{𝐱}_1& {𝐱}_2& \cdots & {𝐱}_i& \cdots & {𝐱}_n\end{array}\right)$なので、

$A{𝐱}_i=d_i{𝐱}_i$（ただし$i=1,2,\cdots ,n$）

ここから、$P$を構成する列ベクトルは$A$の固有ベクトルであり、$P$の対角成分は各固有ベクトルに対応する固有値であることがわかるので、

$P$が正則$⟺$Aの各固有ベクトルが一次独立$⟺\mathrm{d}\mathrm{e}\mathrm{t}P\ne 0$

よって、

$A$が対角化可能$⟺$Aの固有ベクトルを並べた行列Pについて$\mathrm{d}\mathrm{e}\mathrm{t}P\ne 0$

Aが対角化可能なときは、Aのi番目の固有値を${\lambda }_i$とすると$D=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$である。

対角化の検算について、$P^{-1}AP=D$をそのまま用いて検算しようとすると$P^{-1}$を求める必要があるため面倒である。そこで、両辺にPを左から掛けると$AP=PD$となる。これならば容易に計算できる。

• 問題
  • 以下の行列が対角化可能であるか判定し、可能な場合は対角化せよ。
  • 1. $\left(\begin{array}{cc}2& -5\\ 6& 1\end{array}\right)$
  • 2. $\left(\begin{array}{ccc}-1& -9& -3\\ 2& 8& 2\\ -3& -9& -1\end{array}\right)$

連立一次方程式

複数の方程式の左側に{を書いて連立させたものを連立方程式という。 連立させる式が全て一次式の場合は特に連立一次方程式という。 連立させる式の本数がnであるとき、n元連立方程式という。 連立方程式を解くとは、連立させた式を全て満たすように全ての変数の値を定めることである。解が不定になる場合は媒介変数を用いて表す。このとき用いる媒介変数の個数を連立方程式の自由度という。

$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$を計算すると$\left(\begin{array}{c}ax+by\\ cx+dy\end{array}\right)$である。

よって、2変数の2元連立一次方程式

$\{\begin{array}{c}ax+by=p\\ cx+dy=q\end{array}$

は行列を用いて記述すると

$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}p\\ q\end{array}\right)$

となる。

一般に、l変数のn元連立一次方程式は「（n×l行列）（l次列ベクトル） = （n次列ベクトル）」と表せる。このとき、l次行ベクトルの係数となるn×l行列を係数行列という。

つまり、係数行列を$A$、l次列ベクトルを$𝐱$、n次列ベクトルを$𝐛$とおくと、連立一次方程式は

$A𝐱=𝐛$

と表記できる。

この方程式の解はAが正則行列であれば一意に定まり、 $𝐱=A^{-1}𝐛$ である。

2変数の2元連立一次方程式の場合は、係数行列が2次行列になるので逆行列が簡単に求まる。

• 例題
  • $\{\begin{array}{c}ax+by=p\\ cx+dy=q\end{array}$をx,yについて解け。ただし、$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|\ne 0$とする。
  • 解答

$\{\begin{array}{c}ax+by=p\\ cx+dy=q\end{array}$

$⟺\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}p\\ q\end{array}\right)$

$⟺\left(\begin{array}{c}x\\ y\end{array}\right)=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)\left(\begin{array}{c}p\\ q\end{array}\right)(\because \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc\ne 0)$

$⟺\{\begin{array}{c}x=\frac{d}{ad-bc}p-\frac{b}{ad-bc}q\\ y=-\frac{c}{ad-bc}p+\frac{a}{ad-bc}q\end{array}$

一般の連立一次方程式においては、掃き出し法を用いて解を求めることができる。

連立一次方程式$A𝐱=𝐛$の係数行列$A$とn次列ベクトル$𝐛$を横に並べた行列$\left(\begin{array}{cc}A& 𝐛\end{array}\right)$を拡大係数行列という。

ガウスの消去法（掃き出し法）II 

連立一次方程式$A𝐱=𝐛$の拡大係数行列$\left(\begin{array}{cc}A& 𝐛\end{array}\right)$をAに関して簡約化した行列$\left(\begin{array}{cc}{A}^{\prime }& {𝐛}^{\prime }\end{array}\right)$について、$A^{\prime }𝐱={𝐛}^{\prime }$の解は元の方程式の解と一致する。

簡約化とは、任意の行列を行基本変形を繰り返すことによってRREF行列（簡約行列）へ変換することである。

行列のそれぞれの行の最初に現れる0でない成分を行列の主成分といい、RREF行列は以下の4つを満たす行列である。

1. 全ての主成分が1である
2. 主成分を持つ列ベクトルが基本ベクトルである
3. 右側の列ほど主成分が下側にある
4. 全ての成分が0である行が0以外の値を成分に持つ行よりも下側にある

• 例題
  • 連立方程式$\{\begin{array}{c}x+y+3z=5\\ -2x+3y+2z=10\\ 2x+4y+z=32\end{array}$を解け。
• 解答

$\{\begin{array}{c}x+y+3z=5\\ -2x+3y+2z=10\\ 2x+4y+z=32\end{array}⟺\left(\begin{array}{ccc}1& 1& 3\\ -2& 3& 2\\ 2& 4& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{c}5\\ 10\\ 32\end{array}\right)$

拡大係数行列$\left(\begin{array}{cccc}1& 1& 3& 5\\ -2& 3& 2& 10\\ 2& 4& 1& 32\end{array}\right)$に行基本変形を繰り返し用いて、

$\left(\begin{array}{cccc}1& 0& 0& \frac{139}{41}\\ 0& 1& 0& \frac{276}{41}\\ 0& 0& 1& -\frac{70}{41}\end{array}\right)$

よって、

$E\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{c}\frac{139}{41}\\ \frac{276}{41}\\ -\frac{70}{41}\end{array}\right)⟺\{\begin{array}{c}x=\frac{139}{41}\\ y=\frac{276}{41}\\ z=-\frac{70}{41}\end{array}$である。

連立方程式が掃き出し法で解ける原理を簡単に説明する。

基本行列を纏めてSとする。 拡大係数行列に左からSを掛けて$S\left(\begin{array}{cc}A& 𝐛\end{array}\right)=\left(\begin{array}{cc}SA& S𝐛\end{array}\right)$とすることと連立一次方程式$A𝐱=𝐛$に左からSを掛けて$SA𝐱=S𝐛$とすることは同値なので、$SA$ができるだけ簡単になるように簡約化することで、連立方程式が上手く解けるようになる。

完全に簡約化しなくても解が求まる場合がある。 また、解が不定、計算不能である場合もある。

• 例題
  • 次の連立方程式を解け

1. $\{\begin{array}{c}x+2y-z+3w=3\\ 2x+4y+4z+3w=9\\ 3x+6y-z+8w=10\end{array}$

2. $\{\begin{array}{c}a-b+c=3\\ b+c=0\\ 2a+4b+8c=7\end{array}$

• 解答

1. $\{\begin{array}{c}x+2y-z+3w=3\\ 2x+4y+4z+3w=9\\ 3x+6y-z+8w=10\end{array}⟺\left(\begin{array}{cccc}1& 2& -1& 3\\ 2& 4& 4& 3\\ 3& 6& -1& 8\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ w\end{array}\right)=\left(\begin{array}{c}3\\ 9\\ 10\end{array}\right)$

拡大係数行列は$\left(\begin{array}{ccccc}1& 2& -1& 3& 3\\ 2& 4& 4& 3& 9\\ 3& 6& -1& 8& 10\end{array}\right)$である。

行基本変形を繰り返し施して、

$\left(\begin{array}{ccccc}1& 2& -1& 3& 3\\ 2& 4& 4& 3& 9\\ 3& 6& -1& 8& 10\end{array}\right)$

$\to \left(\begin{array}{ccccc}1& 2& -1& 3& 3\\ 0& 0& 6& -3& 3\\ 0& 0& 2& -1& 1\end{array}\right)$

$\to \left(\begin{array}{ccccc}1& 2& -1& 3& 3\\ 0& 0& 2& -1& 1\\ 0& 0& 0& 0& 0\end{array}\right)$

$\to \left(\begin{array}{ccccc}1& 2& 5& 0& 6\\ 0& 0& 2& -1& 1\\ 0& 0& 0& 0& 0\end{array}\right)$

よって、

$\left(\begin{array}{cccc}1& 2& 5& 0\\ 0& 0& 2& -1\\ 0& 0& 0& 0\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ w\end{array}\right)=\left(\begin{array}{c}6\\ 1\\ 0\end{array}\right)⟺\{\begin{array}{c}x+2y+5z=6\\ 2z-w=1\\ 0=0\end{array}$

媒介変数をs,tとすると、解は$\{\begin{array}{c}x=6-2s-5t\\ y=s\\ z=t\\ w=2t-1\end{array}$である。

2. $\{\begin{array}{c}a-b+c=3\\ b+c=0\\ 2a+4b+8c=7\end{array}⟺\left(\begin{array}{ccc}1& -1& 1\\ 0& 1& 1\\ 2& 4& 8\end{array}\right)\left(\begin{array}{c}a\\ b\\ c\end{array}\right)=\left(\begin{array}{c}3\\ 0\\ 7\end{array}\right)$

拡大係数行列は$\left(\begin{array}{cccc}1& -1& 1& 3\\ 0& 1& 1& 0\\ 2& 4& 8& 7\end{array}\right)$である。

行基本変形を繰り返し施して、

$\left(\begin{array}{cccc}1& -1& 1& 3\\ 0& 1& 1& 0\\ 2& 4& 8& 7\end{array}\right)$

$\to \left(\begin{array}{cccc}1& 0& 2& 3\\ 0& 1& 1& 0\\ 2& 4& 8& 7\end{array}\right)$

$\to \left(\begin{array}{cccc}1& 0& 2& 3\\ 0& 1& 1& 0\\ 2& 0& 4& 7\end{array}\right)$

$\to \left(\begin{array}{cccc}1& 0& 2& 3\\ 0& 1& 1& 0\\ 0& 0& 0& 1\end{array}\right)$

よって、

$\left(\begin{array}{ccc}1& 0& 3\\ 0& 1& 1\\ 0& 0& 0\end{array}\right)\left(\begin{array}{c}a\\ b\\ c\end{array}\right)=\left(\begin{array}{c}3\\ 0\\ 1\end{array}\right)⟺\{\begin{array}{c}a+2c=3\\ b+c=0\\ 0=1\end{array}$

$0=1$は成立し得ないので、求める解は存在しない。

連立一次方程式が解を持つ条件を考える。

0でない成分を$*$とするとき、$\left(\begin{array}{cccc}*& \cdots & \cdots & \cdots \\ & *& \cdots & \cdots \\ & & *& \cdots \\ \mathrm{O}& & & \end{array}\right)$の形をした行列を階段行列という。例えば、RREF行列は階段行列である。対角行列のように、$*$の右側に0が入っているものも階段行列と言って良い。

$*$を含む行の個数を階段行列の段数という。

掃き出し法を見ればわかるように、任意の行列は行基本変形を繰り返せば階段行列に変形できる。そこで、階段行列に関連した指標を定義する。

行列の階数（ランク）

任意の行列$A$を行基本変形を用いて階段行列に変換した時、0でない成分が含まれる行の個数を行列の階数（ランク）といい、$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A$と表す。

0でない成分が含まれる行の個数は*を含む行の個数であるため、$A$を変形した階段行列の段数は$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A$に等しい。 また、$A$の列/行ベクトルのうち一次独立なベクトルの最大個数も$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A$に等しくなる。

m×n行列の階数は必ずm,nの小さい方以下になる。

連立一次方程式$A𝐱=𝐛$について、$A$のk番目の列ベクトルを${𝐚}_k$とおく（$1\le k\le n$）。 このとき、$A$の列数と$𝐱$の行数が一致していなければ左辺を計算できないので、$A=\left(\begin{array}{cccc}{𝐚}_1& {𝐚}_2& \cdots & {𝐚}_n\end{array}\right),𝐱=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)$である。

$A𝐱=𝐛$が解を持つとき、$\sum _{k=1}^n{x}_k{𝐚}_k=𝐛$が成り立つ。 これは一次独立なベクトルの一次結合であるため、階数の定義より$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cc}A& 𝐛\end{array}\right)$が成り立つ。

逆に、$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cc}A& 𝐛\end{array}\right)$が成り立つとき、$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=m$とすると$𝐛$は${𝐚}_1,{𝐚}_2,\cdots ,{𝐚}_n$の中から選んだm個の一次独立なベクトルの一次結合で表せ、$𝐛=\sum _{k=1}^n{x}_k{𝐚}_k$となる$𝐱(=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right))$が少なくとも一つ存在する。このとき、$𝐱$は$A𝐱=𝐛$の解そのものである。

よって、

連立一次方程式$A𝐱=𝐛$が解を持つ$⟺\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cc}A& 𝐛\end{array}\right)$

なお、$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A\ne \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cc}A& 𝐛\end{array}\right)$の場合、$\left(\begin{array}{cc}A& 𝐛\end{array}\right)$を簡約化すると最後の行に対応する式は必ず$0=1$という矛盾した式となる。

$A𝐱=𝐛$の解がただ一つである条件を考える。

解がただ一つならば、テンプレート:式番号を満たす$\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)(=𝐱)$が一つに定まる。これは、${𝐚}_k$が一次独立であることを示している。 ${𝐚}_k$が一次独立でないとすると、テンプレート:式番号を満たす$y_k(\ne x_k,0)$が存在し、(1)+(2)より${𝐱}^{\prime }=\left(\begin{array}{c}{x}_1+y_1\\ x_2+y_2\\ ⋮\\ x_n+y_n\end{array}\right)$も連立方程式の解となり、解の一意性に反する。 よって、

解がただ一つ$⟹{𝐚}_k$が一次独立$⟹\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=n$

逆に、$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=n$とすると、 $A𝐱=𝐛,A𝐲=𝐛$について、$A(𝐱-𝐲)=O⟺\sum _{k=1}^n(x_k-y_k){𝐚}_k=O⟺x_k-y_k=0⟺x_k=y_k⟺𝐱=𝐲$

よって、

連立一次方程式$A𝐱=𝐛$がただ一つの解を持つ$⟺\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cc}A& 𝐛\end{array}\right)=n$（ただし、nはAの行数であり、Aの列数以下の値をとる）

このことから、連立一次方程式の式の本数が変数の個数以上のとき、解の個数は0または1であることがわかる。式の本数が変数の個数を下回るとき、解は不定になる。

なお、$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A$は$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cc}A& 𝐛\end{array}\right)$を求める過程で同時に求まる。

連立一次方程式$A𝐱=𝐛$の解が存在するとき、その自由度はちょうど$n-\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A$であることが知られている。この$n$は$A$の列数であり、$𝐱$の行数であり、連立一次方程式の変数の個数である。

• 例題
  • 連立一次方程式$\{\begin{array}{c}x+2y-z+3w=3\\ 2x+4y+4z+3w=9\\ 3x+6y-z+8w=10\end{array}$について、上のことを確かめよ。
• 解答

拡大係数行列は$\left(\begin{array}{ccccc}1& 2& -1& 3& 3\\ 2& 4& 4& 3& 9\\ 3& 6& -1& 8& 10\end{array}\right)$である。

行基本変形を繰り返し施すと、

$\left(\begin{array}{ccccc}1& 2& 5& 0& 6\\ 0& 0& 2& -1& 1\\ 0& 0& 0& 0& 0\end{array}\right)$

よって、

$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cccc}1& 2& -1& 3\\ 2& 4& 4& 3\\ 3& 6& -1& 8\end{array}\right)=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\begin{array}{cccc}1& 2& 5& 0\\ 0& 0& 2& -1\\ 0& 0& 0& 0\end{array}\right)=2$

元の式の変数の個数は4なので、$4-2=2$

これは、先ほど求めたこの連立方程式の解を表すのに使われた媒介変数の個数と一致している。

変数の個数が係数行列の階数に一致するとき、自由度が0なので解は一つに定まる。

連立一次方程式$A𝐱=O$を特に斉次連立一次方程式という。 この方程式について、以下のことが成り立つ。

この方程式が$𝐱=O$（自明解）以外の解（非自明解）を持つ$⟺\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A<n$（ただし、nは方程式の変数の個数）

• 例題
  • 対偶を利用して上記を証明せよ
• 解答

先ほど証明したことから、

$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A=n⟺A𝐱=O$の解がただ1つ$⟺A𝐱=O$の解が自明解のみ

この真なる命題の対偶をとると、

$A𝐱=O$が非自明解を持つ$⟺\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A\ne n$

このとき、$n$は係数行列$A$の列数に等しく、$A$の階数はその定義より必ず$A$の行数と列数の小さい方以下の値をとるため、

$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A\ne n⟺\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A<n$

が成り立つ。 命題とその対偶の真偽は一致するため、命題「$A𝐱=O$が非自明解を持つ$⟺\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A<n$」は真である。

一次変換

一次変換を学ぶ上で大切になるのが、写像と呼ばれる概念である。 以下、写像について簡潔に記す。 テンプレート:コラム これらのことを頭に入れておくと、以下の内容を理解しやすくなるであろう。

連立方程式$A𝐱=𝐛$について、$𝐱,𝐛$はそれぞれ列ベクトルである。 そこで、$𝐱,𝐛$が有向線分$\overrightarrow{x},\overrightarrow{b}$を表すものとしてこの連立方程式を図形的に解釈すると、「$\overrightarrow{x}$に行列$A$を掛けると$\overrightarrow{b}$に移動した」という意味になる。この、ベクトルに行列を掛けて別のベクトルへ移す操作を一次変換という。このとき、行列$A$をこの一次変換の表現行列という。 表現行列が$A$である一次変換を、「$A$で表される一次変換」と呼ぶ。

一次変換を写像とみたとき、これを線形写像という。 $𝔽$を体（元について四則演算が定義されている集合）、$V,W$を$𝔽$の上のベクトル空間（元がベクトルである集合）とする。$f:V\to W$が線形写像ならば、以下を同時に満たす。

1. $f(𝐱+𝐲)=f(𝐱)+f(𝐲)(𝐱,𝐲\in V)$
2. $f(k𝐱)=kf(𝐱)(k\in 𝔽,𝐱\in V)$

この2つの性質は、$f(k𝐱+l𝐲)=kf(𝐱)+lf(𝐲)(k,l\in 𝔽,𝐱,𝐲\in V)$が成り立つことと同値である。この性質を線形性と呼ぶ。 $𝐱,𝐲$を普通の数に置き換えると、シグマ公式・期待値・極限・微分・積分などに見られた性質と一致する。

一次変換は任意のベクトルの一次結合で表すことができる。逆に、定数項が存在すれば線形写像ではない。

線形写像は、$f(x)=ax$のような一次の変換を一般化した写像と言える。$f(x)=a{x}^2$のような二次の変換は線形写像ではない。

$f,g$が線形写像であるならば、その合成$f\circ g,g\circ f$も線形写像である。線形写像$f$が全単射であるならば、その逆写像$f^{-1}$も線形写像であり、これを線形同形という。

Aを線形写像fの表現行列とすると、fの像の次元は$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}A$である。

以下、平面上での一次変換を扱う。

点Pから点Qへの移動は、それぞれの点の位置ベクトルの一次変換と見ることができる。

• 例題
  • 次の行列で表される一次変換によって、点P(1, 3)はどんな点に移るか。

1. $\left(\begin{array}{cc}3& 2\\ 4& 5\end{array}\right)$
2. $\left(\begin{array}{cc}1& 0\\ a& 6\end{array}\right)$

• 解答

1. $\left(\begin{array}{cc}3& 2\\ 4& 5\end{array}\right)\left(\begin{array}{c}1\\ 3\end{array}\right)=\left(\begin{array}{c}9\\ 19\end{array}\right)\therefore P^{\prime }=(9,19)$
2. $\left(\begin{array}{cc}1& 0\\ a& 6\end{array}\right)\left(\begin{array}{c}1\\ 3\end{array}\right)=\left(\begin{array}{c}1\\ a+18\end{array}\right)\therefore P^{\prime }=(1,a+18)$

平面における一次変換は$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$と表される。このとき、$\left(\begin{array}{c}x\\ y\end{array}\right)$は基本ベクトルの一次結合で表され、$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$は$\left(\begin{array}{c}a\\ c\end{array}\right),\left(\begin{array}{c}b\\ d\end{array}\right)$の一次結合で表される。つまり、一次変換は基本ベクトルを任意のベクトルに変換する操作であると言える。

$x,y$が任意の実数値を取り得るとき、ベクトル$\left(\begin{array}{c}x\\ y\end{array}\right)$はxy平面全体を表す。

表現行列$A(=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right))$が正則行列であるとき、$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=A\left(\begin{array}{c}x\\ y\end{array}\right)$の両辺に$A^{-1}$を左から掛けると$\left(\begin{array}{c}x\\ y\end{array}\right)=A^{-1}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$が成り立つ。つまり、任意の$(x^{\prime },y^{\prime })$に対してそれを与える実数$(x,y)$の組が存在する。よって、この表現行列による一次変換は上への写像であり、この変換によって平面全体は平面全体へ移る。また、$\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)\ne \left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)⟹A\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)\ne A\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)(\because$背理法$)$なのでこの変換は全単射である。このように、表現行列が正則行列である一次変換を正則一次変換という。

※「上への写像」とは、$f(X)=Y$が成り立つ写像のことである。（一般に$f:X\to Y$について$f(X)⫅Y$のため）

表現行列$A$が特異行列であるとき、$a=b=c=d=0$ならばこの変換によって平面全体は原点に移る。$\left(\begin{array}{c}a\\ c\end{array}\right)\ne \overrightarrow{0}\vee \left(\begin{array}{c}b\\ d\end{array}\right)\ne \overrightarrow{0}$の場合を考える。$\left(\begin{array}{c}a\\ c\end{array}\right)\ne \overrightarrow{0}$とすると$\left(\begin{array}{c}b\\ d\end{array}\right)=k\left(\begin{array}{c}a\\ c\end{array}\right)$を満たす$k\in ℝ$が存在するので$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=(x+ky)\left(\begin{array}{c}a\\ c\end{array}\right)$が成り立つ。$x+ky\in ℝ$より、この変換によって平面全体は原点を通り方向ベクトルが$\left(\begin{array}{c}a\\ c\end{array}\right)$である直線へ移る。$\left(\begin{array}{c}b\\ d\end{array}\right)\ne \overrightarrow{0}$の場合も同様である。

一次変換同士の合成変換は一次変換である。一次変換$f,g$の表現行列を$A,B$とする。$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=A\left(\begin{array}{c}x\\ y\end{array}\right),\left(\begin{array}{c}{x}^{″}\\ y^{″}\end{array}\right)=B\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$とすると合成変換$h=f\circ g$について$\left(\begin{array}{c}{x}^{″}\\ y^{″}\end{array}\right)=B\left(A\left(\begin{array}{c}x\\ y\end{array}\right)\right)$より$h$の表現行列は$C=BA$である。実は、行列の積を「行ベクトルと列ベクトルの内積を並べたもの」と定義したのは、そうすれば線形写像の合成が表現行列の積に対応するからである。

一次変換の逆変換も一次変換である。上で$C=E$とすると$B=A^{-1},\left(\begin{array}{c}{x}^{″}\\ y^{″}\end{array}\right)=\left(\begin{array}{c}x\\ y\end{array}\right)$なので$\left(\begin{array}{c}x\\ y\end{array}\right)=A^{-1}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$であり、$g=f^{-1}$である。このとき、逆変換の表現行列は元の変換の表現行列の逆行列である。逆行列の公式$(BA{)}^{-1}=A^{-1}{B}^{-1}$より、二つの変換$f,g$がそれぞれ逆変換を持つならばその合成変換$h=f\circ g$も逆変換を持つ。

一次変換の表現行列が$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$であるとき、テンプレート:式番号であるので、$B\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}p\\ r\end{array}\right),B\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}q\\ s\end{array}\right)$とすると$B=\left(\begin{array}{cc}p& q\\ r& s\end{array}\right)$である。ここで$\{\begin{array}{c}A\left(\begin{array}{c}p\\ r\end{array}\right)=\left(\begin{array}{c}k\\ m\end{array}\right)\\ A\left(\begin{array}{c}q\\ s\end{array}\right)=\left(\begin{array}{c}l\\ n\end{array}\right)\end{array}$であるとき、$\{\begin{array}{c}AB\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}k\\ m\end{array}\right)\\ AB\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}l\\ n\end{array}\right)\end{array}$なので、(3)より$AB=\left(\begin{array}{cc}k& l\\ m& n\end{array}\right)$である（このABは、Aの表す変換とBの表す変換の合成変換の表現行列である）。故に、$A=\left(\begin{array}{cc}k& l\\ m& n\end{array}\right)B^{-1}=\left(\begin{array}{cc}k& l\\ m& n\end{array}\right){\left(\begin{array}{cc}p& q\\ r& s\end{array}\right)}^{-1}$である。 このことから、変換の像が2つ与えられたとき、一次変換が決定することがわかる。ただし、変換前の2点の位置ベクトルが一次従属であるとき、最後の計算に使う逆行列が存在しないので表現行列を求められない。また、変換前の2点のいずれかが原点であるときも表現行列を求められない。

• 例題
  • 一次変換$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=A\left(\begin{array}{c}x\\ y\end{array}\right)$によって点(1, 3)、(-1, 5)がそれぞれ点(6, -2)、(3 , 8)に写るとき、表現行列$A$を求めよ。
• 解答

与えられた条件を行列で表すと

$\{\begin{array}{c}A\left(\begin{array}{c}1\\ 3\end{array}\right)=\left(\begin{array}{c}6\\ -2\end{array}\right)\\ A\left(\begin{array}{c}-1\\ 5\end{array}\right)=\left(\begin{array}{c}3\\ 8\end{array}\right)\end{array}$

一つの式に纏めて、

$A\left(\begin{array}{cc}1& -1\\ 3& 5\end{array}\right)=\left(\begin{array}{cc}6& 2\\ -2& 8\end{array}\right)$

よって、

$\therefore A=\left(\begin{array}{cc}6& 2\\ -2& 8\end{array}\right){\left(\begin{array}{cc}1& -1\\ 3& 5\end{array}\right)}^{-1}=\left(\begin{array}{cc}6& 2\\ -2& 8\end{array}\right)\cdot \frac{1}{8}\left(\begin{array}{cc}5& 1\\ -3& 1\end{array}\right)=\frac{1}{8}\left(\begin{array}{cc}24& 8\\ -34& 6\end{array}\right)=\left(\begin{array}{cc}3& 1\\ -\frac{17}{4}& \frac{3}{4}\end{array}\right)$

直線の一次変換について、直線をベクトル方程式表示しておくと線形性を容易に利用できる場合がある。線形性を利用することにより、以下の事実がわかる。

一次変換と線形性

方向ベクトルが零ベクトルでないとき、
①直線は直線へ移る
②平行な2直線は平行な2直線へ移る
③内分点・外分点はその比を変えずに内分点・外分点へ移る。

方向ベクトルが零ベクトルのとき、直線は直線または点へ移る。

また、線形性を利用すると、直線図形は一次変換によって相似な直線図形へ移ることもわかる。

• 例題

表現行列が$A=\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)$で表される一次変換$f$における不動直線を求めよ。ただし、「不動直線」とは、$f$によって自分自身に移る直線である。

• 解答

$\mathrm{d}\mathrm{e}\mathrm{t}A=4\cdot 1-1\cdot (-2)=6$より$f$は正則一次変換なので、$f$によって直線が潰れて点に移ることはない。

①y軸に平行な直線のとき

求める直線は$k\in ℝ$として$x=k$とおけるので、媒介変数をtとすると求める直線のベクトル方程式は

$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}k\\ 0\end{array}\right)+t\left(\begin{array}{c}0\\ 1\end{array}\right)$

である。

方向ベクトルに注目すると、

$A\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}1\\ 1\end{array}\right)//\mathrm{\setminus }\left(\begin{array}{c}0\\ 1\end{array}\right)$

であるので、このタイプの不動直線は存在しない。

②その他の場合

求める直線は$m,n\in ℝ$として$y=mx+n$とおける。

この直線のベクトル方程式は

$\left(\begin{array}{c}x\\ y\end{array}\right)=t\left(\begin{array}{c}1\\ m\end{array}\right)+\left(\begin{array}{c}0\\ n\end{array}\right)$

であり、これを$f$で変換した直線のベクトル方程式は

$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=A\left(\begin{array}{c}x\\ y\end{array}\right)=A\{t\left(\begin{array}{c}1\\ m\end{array}\right)+\left(\begin{array}{c}0\\ n\end{array}\right)\}=tA\left(\begin{array}{c}1\\ m\end{array}\right)+A\left(\begin{array}{c}0\\ n\end{array}\right)$

となる。

$A\left(\begin{array}{c}1\\ m\end{array}\right)\ne \overrightarrow{0}$よりこれが元の直線に一致する条件は、

「$A\left(\begin{array}{c}1\\ m\end{array}\right)//\left(\begin{array}{c}1\\ m\end{array}\right)$」且つ「位置ベクトル$A\left(\begin{array}{c}0\\ n\end{array}\right)$の終点が元の直線上にある」

である。

$A\left(\begin{array}{c}1\\ m\end{array}\right)=\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)\left(\begin{array}{c}1\\ m\end{array}\right)=\left(\begin{array}{c}4+m\\ -2+m\end{array}\right)$より、

$\left(\begin{array}{c}4+m\\ -2+m\end{array}\right)//\left(\begin{array}{c}1\\ m\end{array}\right)⟺\mathrm{d}\mathrm{e}\mathrm{t}\left(\begin{array}{cc}4+m& 1\\ -2+m& m\end{array}\right)=0$

$⟺(m+4)\cdot m-1\cdot (m-2)=0$

$⟺m^2+3m+2=0$

$⟺(m+1)(m+2)=0$

$\therefore m=-1,-2$

$A\left(\begin{array}{c}0\\ n\end{array}\right)=\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)\left(\begin{array}{c}0\\ n\end{array}\right)=\left(\begin{array}{c}n\\ n\end{array}\right)$

この位置ベクトルの表す点が直線$y=mx+n$上にあるので、$n=mn+n$すなわち$mn=0$

$\therefore n=0$

よって求める直線は2本あり、$y=-x$と$y=-2x$である。//

この例題には重要な別解があるので紹介する。

⑴

解答の②において、直線上の点Pを媒介変数表示すると$(t,mt+n)$なので、

$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)\left(\begin{array}{c}t\\ mt+n\end{array}\right)=\left(\begin{array}{c}(m+4)t+n\\ (m-2)t+n\end{array}\right)$

である。

これが元の直線上にあるので、

$(m-2)t+n=m\{(m+4)t+n\}+n=m(m+4)t+mn+n$が$t$の恒等式である。

故に$\{\begin{array}{c}m-2=m^2+4m\\ n=mn+n\end{array}$より

$\{\begin{array}{c}m=-1,-2\\ n=0\end{array}$が導かれる。

⑵

$f$によって方向の変わらないベクトルを求める。

$A\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}4x+y\\ -2x+y\end{array}\right)$より、

$A\left(\begin{array}{c}x\\ y\end{array}\right)//\left(\begin{array}{c}x\\ y\end{array}\right)⟺\mathrm{d}\mathrm{e}\mathrm{t}\left(\begin{array}{cc}4x+y& x\\ -2x+y& y\end{array}\right)=0$

$⟺(4x+y)y-x(-2x+y)=0$

$⟺2x^2+3xy+y^2=0$

$⟺(2x+y)(x+y)=0$

$⟺y=-x,-2x$

よって求めるベクトルは$\left(\begin{array}{c}1\\ -1\end{array}\right),\left(\begin{array}{c}1\\ -2\end{array}\right)$である。

これにより、求める直線の傾きは$m=-1,-2$とわかる。あとは条件から定数項が0であることを示せば良い。

勘と記憶力の良い読者は気づいたかもしれないが、上で求めた$f$により方向の変わらないベクトルは表現行列$A$の固有ベクトルに等しい（「行列式・固有値」節の例題で$\left(\begin{array}{cc}4& 1\\ -2& 1\end{array}\right)$の固有ベクトルを既に求めた）。これは一般の一次変換に言える事実である。

この方法では、直線の傾きによる場合分けが不要である。つまり、一次変換における不動直線を求めたいならばまず表現行列の固有ベクトルを求めよう。

• 問題

直線図形が表現行列$A$の一次変換$f$により移った直線図形の面積が元の$|\mathrm{d}\mathrm{e}\mathrm{t}A|$倍であることを証明せよ。ただし、直線図形が全て種々の三角形の組み合わせで表現できることを用いて良い。

以下、種々の一次変換の表現行列を求めていく。ただし、各操作が一次変換であることの証明は省いた。

一次変換$\left(\begin{array}{c}x\\ y\end{array}\right)\to \left(\begin{array}{c}\alpha x\\ \beta y\end{array}\right)$は「x軸方向にα倍、y軸方向にβ倍」することを意味する。このような変換を「軸方向の伸縮」という。

行列の積を考えると、伸縮の表現行列は$\left(\begin{array}{cc}\alpha & 0\\ 0& \beta \end{array}\right)$であることが容易にわかる。

$\alpha ,\beta$に具体的な値を入れると以下のようになる。

$\alpha =1,\beta =-1$：x軸に対する対称移動

$\alpha =-1,\beta =1$：y軸に対する対称移動

$\alpha =\beta =-1$：原点に対する対称移動

$\alpha =\beta$：原点を中心とするα倍の伸縮（相位変換）

$\alpha =\beta =1$：恒等変換

恒等変換は普通$e$と書く。$e$の表現行列は単位行列$E$である。

$\left(\begin{array}{cc}1& \alpha \\ \beta & 1\end{array}\right)$で表される一次変換はどのような変換であろうか。

$\left(\begin{array}{cc}1& \alpha \\ \beta & 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}x+\alpha y\\ \beta x+y\end{array}\right)$より、これはx軸方向・y軸方向それぞれのズレを表す行列である。

原点中心の$\theta$回転の表現行列を求める。

$P(x,y)$を原点中心にθ回転した先の点を$P^{\prime }(x^{\prime },y^{\prime })$、この一次変換を$f$とおく。基本ベクトルを${\overrightarrow{e}}_x,{\overrightarrow{e}}_y$とすると、$\overrightarrow{OP}=x{\overrightarrow{e}}_x+y{\overrightarrow{e}}_y$である。

よって、$\overrightarrow{O{P}^{\prime }}=f(\overrightarrow{OP})=f(x{\overrightarrow{e}}_x+y{\overrightarrow{e}}_y)=xf({\overrightarrow{e}}_x)+yf({\overrightarrow{e}}_y)$

$f({\overrightarrow{e}}_x)={\overrightarrow{e^{\prime }}}_x,f({\overrightarrow{e}}_y)={\overrightarrow{e^{\prime }}}_y$とおく。

単位円上に${\overrightarrow{e}}_x,{\overrightarrow{e}}_y,{\overrightarrow{e^{\prime }}}_x,{\overrightarrow{e^{\prime }}}_y$を図示すると、${\overrightarrow{e^{\prime }}}_x,{\overrightarrow{e^{\prime }}}_y$がx軸となす角はそれぞれ$\theta ,\theta +\frac{\pi }{2}$である。

よって三角関数の定義より${\overrightarrow{e^{\prime }}}_x=\left(\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right),{\overrightarrow{e^{\prime }}}_y=\left(\begin{array}{c}\cos (\theta +\frac{\pi }{2})\\ \sin (\theta +\frac{\pi }{2})\end{array}\right)=\left(\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right)$

$\therefore \overrightarrow{O{P}^{\prime }}=x\left(\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right)+y\left(\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

すなわち、求める表現行列は$\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$である。

表現行列$\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$を回転行列といい、$R(\theta )$や$R_{\theta }$のように表す。

回転行列は三角関数の加法定理からも導出できる。逆に、回転行列を用いて加法定理を導出することもできる。

直線$l:y=mx$に関する対称移動の表現行列を求める。

移動前の点を$P(\overrightarrow{x})$、移動後の点を$P^{\prime }(\overrightarrow{x^{\prime }})$、直線$l$の単位方向ベクトルを$\overrightarrow{e}$とする。

$P$から$l$に下ろした垂線の足を$H$とすると、正射影ベクトルの公式より$\overrightarrow{OH}=(\overrightarrow{e}\cdot \overrightarrow{x})\overrightarrow{e}$

$H$は$P{P}^{\prime }$の中点なので、$\overrightarrow{OH}=\frac{\overrightarrow{x}+\overrightarrow{x^{\prime }}}{2}$

$\therefore \overrightarrow{x^{\prime }}=2\overrightarrow{OH}-\overrightarrow{x}=2(\overrightarrow{e}\cdot \overrightarrow{x})\overrightarrow{e}-\overrightarrow{x}$

$l$の方向ベクトルを$\overrightarrow{m}=\left(\begin{array}{c}1\\ m\end{array}\right)$とおくと、

$\overrightarrow{e}=\frac{\overrightarrow{m}}{|\overrightarrow{m}|}=\frac{1}{\sqrt{1+m^2}}\left(\begin{array}{c}1\\ m\end{array}\right),\overrightarrow{x}=\left(\begin{array}{c}x\\ y\end{array}\right),\overrightarrow{x^{\prime }}=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right),\overrightarrow{e}\cdot \overrightarrow{x}=\frac{x+my}{\sqrt{1+m^2}}$なので、

$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=2\cdot \frac{x+my}{\sqrt{1+m^2}}\cdot \frac{1}{\sqrt{1+m^2}}\left(\begin{array}{c}1\\ m\end{array}\right)-\left(\begin{array}{c}x\\ y\end{array}\right)$

$=\frac{2}{1+m^2}\left(\begin{array}{c}x+my\\ mx+m^{2}y\end{array}\right)-\left(\begin{array}{c}x\\ y\end{array}\right)$

$=\frac{2}{1+m^2}\left(\begin{array}{cc}1& m\\ m& m^2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)-\frac{1+m^2}{1+m^2}\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

$=\frac{1}{1+m^2}\{\left(\begin{array}{cc}2& 2m\\ 2m& 2m^2\end{array}\right)-\left(\begin{array}{cc}1+m^2& 0\\ 0& 1+m^2\end{array}\right)\}\left(\begin{array}{c}x\\ y\end{array}\right)$

$=\frac{1}{1+m^2}\left(\begin{array}{cc}1-m^2& 2m\\ 2m& -1+m^2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

すなわち、求める表現行列は$\frac{1}{1+m^2}\left(\begin{array}{cc}1-m^2& 2m\\ 2m& -1+m^2\end{array}\right)$である。

$l$の方向ベクトルを$\overrightarrow{m}=\left(\begin{array}{c}a\\ b\end{array}\right)$のようにとると、表現行列は$\frac{1}{a^2+b^2}\left(\begin{array}{cc}{a}^2-b^2& 2ab\\ 2ab& b^2-a^2\end{array}\right)$となる。

また、上の計算過程から、$\overrightarrow{OH}=\frac{1}{1+m^2}\left(\begin{array}{cc}1& m\\ m& m^2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\frac{1}{a^2+b^2}\left(\begin{array}{cc}{a}^2& ab\\ ab& b^2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$と求まる。これは点$P$の$l$への正射影を表すベクトルなので、直線$y=mx$への正射影の表現行列は$\frac{1}{1+m^2}\left(\begin{array}{cc}1& m\\ m& m^2\end{array}\right)=\frac{1}{a^2+b^2}\left(\begin{array}{cc}{a}^2& ab\\ ab& b^2\end{array}\right)$である。

回転行列による変換では、図形の形・面積ともに保存される。回転行列は${}^t{R}_{\theta }{R}_{\theta }=E$を満たすので直交行列である。二次において、直交行列は$E,\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),R_{\theta },\left(\begin{array}{cc}\cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array}\right)$などが存在する。

直交行列$M$の各列ベクトルは大きさが1かつ互いに直交し、$|\mathrm{d}\mathrm{e}\mathrm{t}M|=1$を満たす。

すなわち、一般に直交行列による変換では図形の形・面積が保存される（合同変換）。直交行列による変換は直交変換という。

$P^2=P$を満たす正方行列を射影行列または冪等行列という。

例えば、$\left(\begin{array}{cc}1& 1\\ 0& 0\end{array}\right)$は射影行列である。

射影行列$P$に対して$P\overrightarrow{a}=\overrightarrow{b}$とすると、媒介変数を$t$として$P(t\overrightarrow{a}+(1-t)\overrightarrow{b})=tP\overrightarrow{a}+(1-t)P\overrightarrow{b}=t\overrightarrow{b}+(1-t)P^2\overrightarrow{a}=t\overrightarrow{b}+(1-t)P\overrightarrow{a}=t\overrightarrow{b}+(1-t)\overrightarrow{b}=\overrightarrow{b}$である。

つまり、射影行列による変換で点$A(\overrightarrow{a})$が点$B(\overrightarrow{b})$に移るとき、直線$AB$上にある点は全て点$B$に移る。

対称行列である射影行列を直交射影行列という。

例えば、$P=\left(\begin{array}{cc}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& \frac{1}{2}\end{array}\right)$は$P^2=P\wedge {}^{t}P=P$なので直交射影行列である。

直交射影行列$P$に対して$P\overrightarrow{a}=\overrightarrow{b}$とすると、$(\overrightarrow{b}-\overrightarrow{a}){}^t\overrightarrow{b}=(P\overrightarrow{a}-\overrightarrow{a}){}^t(P\overrightarrow{a})=\overrightarrow{a}{}^{t}P{}^t(P\overrightarrow{a})-\overrightarrow{a}{}^t(P\overrightarrow{a})=\overrightarrow{a}{}^t(P\overrightarrow{a})-\overrightarrow{a}{}^t(P\overrightarrow{a})=0$である。

※$\overrightarrow{a},\overrightarrow{b}$が列ベクトル同士もしくは行ベクトル同士ならば、$\overrightarrow{a}{}^t\overrightarrow{a},\overrightarrow{a}{}^t\overrightarrow{b},\overrightarrow{b}{}^t\overrightarrow{a},\overrightarrow{b}{}^t\overrightarrow{b}$は行列の積として計算可能である。また、その計算結果はベクトルではなく一次行列である。

ここから、直交射影行列による一次変換で点$A(\overrightarrow{a})$が点$B(\overrightarrow{b})$に移るとき、$\overrightarrow{AB}\perp \overrightarrow{b}$であることがわかる。

一般に、${\overrightarrow{a}}_1,\cdots ,{\overrightarrow{a}}_n$が空間$V$の基底（後述）であり、$A$を$\overrightarrow{a_i}$の並んだ行列とすると、$\mathrm{d}\mathrm{e}\mathrm{t}({}^{t}AA)\ne 0$のとき$V$上の直交射影行列$P$は$P=A({}^{t}AA{)}^{-1}{}^{t}A$である。

最小二乗法において、$|A\overrightarrow{x}-\overrightarrow{b}|$を最小にする$\overrightarrow{x}$は正規方程式${}^{t}AA\overrightarrow{x}={}^{t}A\overrightarrow{b}$を解く、すなわち$\overrightarrow{x}=({}^{t}AA{)}^{-1}{}^{t}A\overrightarrow{b}$を計算することでただ一つ求まる。

一次変換の観点から見ると、「表現行列$A$の表す一次変換による$\overrightarrow{x}$の像と$\overrightarrow{b}$が近づくようにしたい」ので、「$A\overrightarrow{x}$が$\overrightarrow{b}$を直交射影変換した像に等しく」なれば良い。すなわち、$A\overrightarrow{x}=P\overrightarrow{b}=A({}^{t}AA{)}^{-1}{}^{t}A\overrightarrow{b}$が成り立てば良い。ここから、正規方程式の解が導出される。

• 例題

x軸となす正の角が$\theta$である直線に関する対称移動の表現行列を求めよ。

• 解答

直線を原点中心に$-\theta$回転すると$x$軸に一致することから、この一次変換は$-\theta$回転、$x$軸に関する対称移動、$\theta$回転という3つの一次変換の合成変換である。よって、求める表現行列は

$\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)={\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)}^2=\left(\begin{array}{cc}{\cos }^2\theta -{\sin }^2\theta & 2\sin \theta \cos \theta \\ 2\sin \theta \cos \theta & {\sin }^2\theta -{\cos }^2\theta \end{array}\right)=\left(\begin{array}{cc}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{array}\right)$

※複数の行列の積は右から計算するため、最初に行う変換の表現行列を右端に持ってくる。

一般の点に関する回転は、「回転の中心となる点を原点に重ねる平行移動をする」「原点に関して回転する」「平行移動したものを元に戻す」という3つの変換の合成変換である。複素数平面における回転も同様の考え方を用いている。しかし、平行移動は一次変換ではないので、これらの操作の合成を表現行列の積として表すことはできない。

平行移動が一次変換でないことは以下のように示される。

一次変換は$𝐛=A𝐱$という形式で表される写像である。平行移動によってベクトル$\left(\begin{array}{c}0\\ 0\end{array}\right)$

は自身を除く任意のベクトルに変換されるが、全ての表現行列$A$に対して$A\left(\begin{array}{c}0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$が成り立つので、平行移動に対応する表現行列は存在しない。すなわち、平行移動は一次変換ではない。//

そこで、位置ベクトルの考え方を利用する。

$A(a,b)$を中心とする$\theta$回転で$P(x,y)$が$Q(x^{\prime },y^{\prime })$に移ったとする。$P,Q$の位置ベクトルを求めると$\overrightarrow{OP}=\left(\begin{array}{c}x-\alpha \\ y-\beta \end{array}\right),\overrightarrow{OQ}=\left(\begin{array}{c}{x}^{\prime }-\alpha \\ y^{\prime }-\beta \end{array}\right)$であり、原点を中心とする$\theta$回転で前者が後者に移されるので、$\overrightarrow{OQ}=R(\theta )\overrightarrow{OP}$すなわち$\left(\begin{array}{c}{x}^{\prime }-\alpha \\ y^{\prime }-\beta \end{array}\right)=R(\theta )\left(\begin{array}{c}x-\alpha \\ y-\beta \end{array}\right)$である。変形すると、$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=R(\theta )\left(\begin{array}{c}x-\alpha \\ y-\beta \end{array}\right)+\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)$すなわち$\overrightarrow{OQ}=R(\theta )\overrightarrow{AP}+\overrightarrow{OA}$である。ちなみに、これをもう一度変形すると$\overrightarrow{AQ}=R(\theta )\overrightarrow{AP}$、つまりAがベクトルの始点である。

これを利用すると、多角形の一つの頂点に関する回転移動を考えることができる。なお、一般の点に関する回転も次元を一つあげれば行列の積を用いて表現することが可能である。詳細は後述する。

n次元空間上の全ての点を表現できる且つ表現の仕方が重複しないn次元ベクトルの組を基底という。方向の違うn個のn次元ベクトルの組はすべて基底となり得るので、一次以上のベクトル空間に対して基底となるベクトルの組合せは無数に存在する。一般に、n次ベクトル空間上の基底は、必ずn本の一次独立なベクトルの組から構成される。

$A\sim B$であるならば、Aの表す線形写像とBの表す線形写像は基底のとり方が異なるだけで同じものである。 よって、表現行列と相似な行列を見つければ、線形写像をより簡潔に記述できる可能性がある。

アフィン変換

一次変換では原点を中心とした回転移動を見てきたが、先述のように平行移動は表現行列の積のみで表すことができないので一般の点を中心とした回転移動は一次変換の知識だけでは扱うことができない。そこで、平行移動を行列の積で表す方法を考える。

結論から言うと、拡大係数行列を用いるとうまくいく。 一般に、$\left(\begin{array}{c}y\\ 1\end{array}\right)=\left(\begin{array}{ccc}& A& \\ 0& \cdots & 0\end{array}\right)\left(\begin{array}{cc}x& 1\end{array}\right)$はベクトルの平行移動を表す。

実は、数学C「ベクトル」で扱った内容はベクトルの平行移動を考えているため、厳密にはベクトル空間上ではなくアフィン空間上の議論である。

※（以下執筆中）