高等学校物理基礎/力学

小学校・中学校・高等学校の学習＞高等学校の学習＞高等学校理科 物理基礎

物体の運動

位置と変位

ファイル:高校物理I 等速直線運動 平均の速度.svg

変位

直線上を物体が運動するとき，直線に沿って座標軸($x$軸)をとることで物体の位置(テンプレート:Lang-en-short)を表せる。物体の位置変化を変位(テンプレート:Lang-en-short)といい，時刻$t_1,t_2(t_1<t_2)$〔単位：s(秒)〕における物体の位置がそれぞれ$x_1,x_2$〔単位：m(メートル)〕であるとき，変位$\mathrm{\Delta }x$は

$\mathrm{\Delta }x=x_2-x_1$

であり。変位の大きさが２点間距離を表し，正負の符号が移動方向を表す。

速度

速さ

物体が運動するとき, その移動距離を経過時間で割ったもの, すなわち単位時間あたりの移動距離を速さ(テンプレート:Lang-en-short)という。速さにおいては向きを考えない。運動している物体の移動距離を$s$, 経過時間を$\mathrm{\Delta }t$とすると, 物体の速さ$v$は次のように表される。

$v=s÷\mathrm{\Delta }t=\frac{s}{\mathrm{\Delta }t}$. (1.1)

速さの単位は時間と距離の単位によって決まる。よく用いられるのは, m/s(メートル毎秒)である。また, 日常生活では距離の単位をkm(キロメートル), 時間の単位をh(時)とするkm/h(キロメートル毎時)もよく使われる。

速度

速さが同じでも向きが異ならば異なる方向に進む。運動の様子を知るには速さだけでなく向きも考えねばならない。速さに向きの要素を加えたもの，すなわち単位時間あたりの変位を速度(テンプレート:Lang-en-short)という。たとえば、西へ走る40㎞/hの車Aと東へ走る40㎞/hの車Bは速さは等しいが、向きは反対である。このことを表すために正負の記号を利用する。つまり、西を正・東を負とするとAの速度は+40㎞/h, Bの速度は-40㎞/hと表記できる。

このように大きさと向きを持つ量をベクトル(テンプレート:Lang-en-short, 独: Vektor)といい, その記号は$\overrightarrow{v}$と書く。ただし, 先ほどのように直線上(１次元)においては速度の値に±が書かれている場合には矢印を省略して単に$v$と書いてもよい。逆に，速さのように大きさのみを持つ量をスカラー(テンプレート:Lang-en-short)という。

なお，平面(２次元)・空間(３次元)上の運動や高度な運動の表し方等は後程説明する。

平均速度と瞬間速度

平均速度と瞬間速度

時刻$t_1$[s]における位置を$x_1$[m], 時刻$t_2$[s]における位置を$x_2$[m](ただし$t_1<t_2$)としたとき, 位置の変位は$x_2-x_1=\mathrm{\Delta }x$, 経過時間は$t_2-t_1=\mathrm{\Delta }t$で表される。このとき,

$\overline{v}=\frac{x_2-x_1}{t_2-t_1}=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}$. (1.2)

(1.2)はある区間における単位時間あたりの変位を表している。こうして求められる速度を平均速度$\overline{v}$(バーvと読む)という。なお，(1.1)で得られた速さも経過時間における平均の速さである。

このとき$\mathrm{\Delta }t$の値を極めて小さくする(すなわち$t_2$を限りなく$t_1$に近づける)と平均速度$\overline{v}$は時刻$t_1$における瞬間速度を表す。時刻$t$における瞬間速度$v$は以下のように位置$x$の一階微分で求められる。

$v=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=\frac{dx}{dt}$.

普通，速度(速さ)は瞬間速度(速さ)をさす。自動車などの速度計に代表される速さの測定器で表示される数値は瞬間の速さである。

等速直線運動

• 
  等速直線運動 x-t グラフ
• 
  等速直線運動 v-t グラフ

一直線上を一定の速さで進む運動を等速直線運動（テンプレート:Lang-en-short）あるいは等速度運動（テンプレート:Lang-en-short）という。時刻$t$において位置$x(0)$から$+x$方向に速度$v$で等速直線運動した物体の位置$x(t)$は($x(t)$は$x$が時刻$t$の関数であることを表す)

$x(t)=\int vdt=vt+C$. ($C$は積分定数)

時刻$t=0$において

$x(0)=v\cdot 0+C=C⟺C=x(0)$.

したがって

$x(t)=x(0)+vt$

となる。この初期位置$x(0)$は初期条件(テンプレート:Lang-en-short)である。なお，変位$\mathrm{\Delta }x=x(t)-x(0)$とおくと

$\mathrm{\Delta }x=vt$.

速度の合成と分解

流れるプールや動く歩道(エスカレーター)を想像すると，流れに乗って動くときと流れに逆らって動くときでは感覚が違うであろう。動く歩道上を(動く歩道の進行方向と同じ向きに)歩く人の速さは，静止歩道上に歩く人の速さよりも大きくなる。これは歩行速度に動く歩道の速度が加わるからである。

直線上での速度の合成

船が川の流れに対して平行に進んでいる場合を考える。静水中の船の速度を$v_1$，地面に対する川の水の流れの速度を$v_2$とするとき，地面に対する船の速度$v$は次式で表される。

$v=v_1+v_2$.

物体の速度$v$が上式のように表されるとき，速度$v$を$v_1$と$v_2$との合成速度といい，合成速度を求めることを速度の合成という。直線上の運動では，どの向きを正とするかを考えてから速度の和を取る。

平面上(２次元)での速度の合成

速度の合成

水が流れている川の上を横切ろうとする船を考える。流水中でも静水中と同じ出力で船が動く場合，静水中での速度が$\overrightarrow{v_1}$の船が水の流れる速度が$\overrightarrow{v_2}$である川の上を横切るとき，地面に対する船の速度$v$は次式で表される。

$\overrightarrow{v}=\overrightarrow{v_1}+\overrightarrow{v_2}$. (1.3)

右図のように，川の流れの速さのぶんだけ船は下流に流される。よって，合成速度の向きは図のように斜めの方向になる。

速度の分解

(1.3)は速度$\overrightarrow{v}$を速度$\overrightarrow{v_1},\overrightarrow{v_2}$に分ける式と考えることもできる。このような見方を速度の分解といい，分解された速度$\overrightarrow{v_1},\overrightarrow{v_2}$を分速度という。

２次元において，速度$\overrightarrow{v}$をたがいに垂直な座標軸である$x$軸，$y$軸方向へ分解し，それぞれの分速度を$\overrightarrow{v_x},\overrightarrow{v_y}$とする。分速度$\overrightarrow{v_x},\overrightarrow{v_y}$の大きさに座標軸の向きを表す正負の符号をつけたものを，$\overrightarrow{v}$の$x$成分，$y$成分といい，それぞれ$v_x,v_y$とすると，$\overrightarrow{v}=(v_x,v_y)$と表せる。このとき，$\overrightarrow{v}$の大きさ(速さ)を$v,\overrightarrow{v}$と$x$軸とのなす角を$\theta$とすると

$v_x=v\cos \theta ,v_y=v\sin \theta ,v=\sqrt{{v_x}^2+{v_y}^2}$.

相対速度

相対速度 電車の中から見た場合

動く物体Aから観測した他の物体Bの速度のことを，Aに対するBの相対速度(テンプレート:Lang-en-short)という。観測者の速度が基準である。

動いている電車の中に観測者がおり，外は雨が降っているとする。電車の中の観測者から見て，雨の速度はどう見えるか? 雨の方向と電車の動く方向とが違う為，ベクトルで考える必要がある。

電車の速度を$\overrightarrow{v_{\text{A}}}$とし，雨の速度（つまり雨の落下速度）を$\overrightarrow{v_{\text{B}}}$ とする。この関係をベクトルで表記すると

$\overrightarrow{v_{\text{AB}}}=\overrightarrow{v_{\text{B}}}-\overrightarrow{v_{\text{A}}}$.

加速度

平均加速度と瞬間加速度

速度のグラフの傾き，ある瞬間の速度の増減の度合い，すなわち，単位時間あたりの速度変化を加速度(テンプレート:Lang-en-short)〔単位：m/s$2^{}$(メートル毎秒毎秒)〕という。

時刻$t_1$での速度を$v_1$，時刻$t_2$での速度を$v_2$とした場合，単位時間当たりの速度の変化量を表す平均加速度$\overline{a}$は次式で表される。

$\overline{a}=\frac{v_2-v_1}{t_2-t_1}=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}$.

このとき$\mathrm{\Delta }t$の値を極めて小さくする(すなわち$t_2$を限りなく$t_1$に近づける)と平均加速度$\overline{a}$は時刻$t_1$における瞬間加速度を表す。普通，加速度は瞬間加速度をさす。時刻$t$における(瞬間)加速度$a$は以下のように速度$v$の一階微分又は位置$x$の二階微分で求められる。

$a=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{dv}{dt}=\frac{d^{2}x}{d{t}^2}$. (1.4)

等加速度直線運動

滑らかな斜面上で物体を静かに放すと物体は一定加速度で直線運動する。このような運動を等加速度直線運動(テンプレート:Lang-en-short)という。

加速度$a$で等加速度直線運動をしている物体を考える。時刻$t$における物体の速度$v(t)$は

$v(t)=\int adt=at+C_1$. ($C_1$は積分定数)

時刻$t=0$において

$v(0)=a\cdot 0+C_1=C_1⟺C_1=v(0)$.

したがって

$v(t)=v(0)+at$ (1.5)

となる。更に，時刻$t$における物体の位置$x(t)$は

$x(t)=\int v(t)dt=\int (v(0)+at)dt=v(0)t+\frac{1}{2}a{t}^2+C_2$. ($C_2$は積分定数)

時刻$t=0$において

$x(0)=v(0)\cdot 0+\frac{1}{2}a\cdot 0^2+C_2=C_2⟺C_2=x(0)$.

したがって

$x(t)=x(0)+v(0)t+\frac{1}{2}a{t}^2$ (1.6)

となる。これら初速度$v(0)$，初期位置$x(0)$は初期条件である。

また，(1.5)を変形すると

$t=\frac{v(t)-v(0)}{a}$

が得られ，これを(1.6)に代入すると

$x=x(0)+v(0)\frac{v(t)-v(0)}{a}+\frac{1}{2}a{\left(\frac{v(t)-v(0)}{a}\right)}^2\therefore v(t{)}^2-v(0{)}^2=2a(x(t)-x(0))$ (1.7)

が得られる。なお，変位$\mathrm{\Delta }x=x(t)-x(0)$とおくと，(1.6), (1.7)は

$\mathrm{\Delta }x=v(0)t+\frac{1}{2}a{t}^2$

$v(t{)}^2-v(0{)}^2=2a\mathrm{\Delta }x$

に変形できる。

２次元・３次元における位置・速度・加速度

時刻$t$における位置は２次元においては$\overrightarrow{r}(t)=(x(t),y(t))$，３次元においては$\overrightarrow{r}(t)=(x(t),y(t),z(t))$と定義される。以下では主に３次元の場合を中心に説明する。

時刻$t$における位置は$\overrightarrow{r}(t)=(x(t),y(t),z(t))$，微小時間$\mathrm{\Delta }t$間の変位は$\mathrm{\Delta }\overrightarrow{r}=\overrightarrow{r}(t+\mathrm{\Delta }t)-\overrightarrow{r}(t)=(\mathrm{\Delta }x,\mathrm{\Delta }y,\mathrm{\Delta }z)$と定義される。このとき

$\overline{\overrightarrow{v}}=\frac{\overrightarrow{r}(t+\mathrm{\Delta }t)-\overrightarrow{r}(t)}{\mathrm{\Delta }t}=\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}$

を$\mathrm{\Delta }t$間の平均速度，$\mathrm{\Delta }t\to 0$の極限

$\overrightarrow{v}(t)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\overrightarrow{r}(t+\mathrm{\Delta }t)-\overrightarrow{r}(t)}{\mathrm{\Delta }t}=\frac{d\overrightarrow{r}(t)}{dt}=(\frac{dx(t)}{dt},\frac{dy(t)}{dt},\frac{dz(t)}{dt})=(v_x(t),v_y(t),v_z(t))$ (1.8)

を時刻$t$での(瞬間)速度という。なお，時刻$t$での速さ(速度の大きさ)は

$v(t)=|\overrightarrow{v}(t)|=\sqrt{v_x(t{)}^2+v_y(t{)}^2+v_z(t{)}^2}$.

この場合も，速度から位置が求まり，各成分毎に

$x(t)=x(0)+\underset{0}{\overset{t}{\int }}{v}_x(t)dt$

$y(t)=y(0)+\underset{0}{\overset{t}{\int }}{v}_y(t)dt$

$z(t)=z(0)+\underset{0}{\overset{t}{\int }}{v}_z(t)dt$

が成り立ち，これらをベクトルを用いてひとまとめにして任意の時刻$t$における位置

$\overrightarrow{r}(t)=\overrightarrow{r}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{v}(t)dt$ (1.9)

が求められる。

また，

$\overline{\overrightarrow{a}}=\frac{\overrightarrow{v}(t+\mathrm{\Delta }t)-\overrightarrow{v}(t)}{\mathrm{\Delta }t}=\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}$ ($\mathrm{\Delta }\overrightarrow{v}$は微小時間$\mathrm{\Delta }t$間の速度変化)

を$\mathrm{\Delta }t$間の平均加速度，$\mathrm{\Delta }t\to 0$の極限

$\begin{array}{cc}\overrightarrow{a}(t)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\overrightarrow{v}(t+\mathrm{\Delta }t)-\overrightarrow{v}(t)}{\mathrm{\Delta }t}& =\frac{d\overrightarrow{v}(t)}{dt}=(\frac{d{v}_x(t)}{dt},\frac{d{v}_y(t)}{dt},\frac{d{v}_z(t)}{dt})\\ & =\frac{d^2\overrightarrow{r}(t)}{d{t}^2}=(\frac{d^{2}x(t)}{d{t}^2},\frac{d^{2}y(t)}{d{t}^2},\frac{d^{2}z(t)}{d{t}^2})\end{array}$ (1.10)

を時刻$t$での(瞬間)加速度という。 この場合も，加速度から速度が求まり，各成分毎に

$v_x(t)=v_x(0)+\underset{0}{\overset{t}{\int }}\frac{d{v}_x(t)}{dt}dt$

$v_y(t)=v_y(0)+\underset{0}{\overset{t}{\int }}\frac{d{v}_y(t)}{dt}dt$

$v_z(t)=v_z(0)+\underset{0}{\overset{t}{\int }}\frac{d{v}_z(t)}{dt}dt$

が成り立ち，これらをベクトルを用いてひとまとめにして任意の時刻$t$における速度

$\overrightarrow{v}(t)=\overrightarrow{v}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{a}(t)dt$ (1.11)

が求められる。なお，これら初期条件$\overrightarrow{r}(0),\overrightarrow{v}(0)$の値を初期値という。

特に，加速度一定のときの運動は等加速度運動(テンプレート:Lang-en-short)といわれ，上記の公式(1.11, 9)はそれぞれ

$\{\begin{array}{c}\overrightarrow{v}(t)=\overrightarrow{v}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{a}dt=\overrightarrow{v}(0)+\overrightarrow{a}t\\ \overrightarrow{r}(t)=\overrightarrow{r}(0)+\underset{0}{\overset{t}{\int }}(\overrightarrow{v}(0)+\overrightarrow{a}t)dt=\overrightarrow{r}(0)+\overrightarrow{v}(0)t+\frac{1}{2}\overrightarrow{a}{t}^2\end{array}$ (1.12)

となる。

落体の運動

自由落下

重力だけが働いて初速度0で落下する運動を自由落下という。

鉛直投射

鉛直投げ下ろし

鉛直下向きに$y$軸をとり，投げ下ろした時刻を$t=0$として，物体を投げ下ろした位置を$y_0$，初速度の大きさを$v_0$，時刻$t$における物体の速度を$v$，位置を$y$とすると，加速度は重力加速度$g$であるから

$v=v_0+gt$

$y=y_0+v_{0}t+\frac{1}{2}g{t}^2$

$v^2-v_0^2=2g(y-y_0)$

が得られる。なお，物体の初速度の大きさ$v_0=0$，すなわち物体が前述の自由落下運動をするとき，上３式は

$v=gt$

$y=y_0+\frac{1}{2}g{t}^2$

$v^2=2g(y-y_0)$

となり，自由落下の式が得られる。

鉛直投げ上げ

鉛直上向きに$y$軸をとり，投げ上げた時刻を$t=0$として，物体を投げ上げた位置を$y_0$，初速度の大きさを$v_0$，時刻$t$における物体の速度を$v$，位置を$y$とすると，加速度は重力加速度$-g$であるから

$v=v_0-gt$

$y=y_0+v_{0}t-\frac{1}{2}g{t}^2$

$v^2-v_0^2=-2g(y-y_0)$

が得られる。

水平投射

物体をある高さから水平方向に投げ出すことを水平投射という。

物体を水平方向に初速度の大きさ$v_0$で投げ出したときの運動を考える。初速度の向きに$x$軸，鉛直下向きに$y$軸をとり，時刻$t$における物体の位置を$\overrightarrow{r}(t)=(x(t),y(t))$，速度を$\overrightarrow{v}(t)=(v_x(t),v_y(t))$とする。物体を投げ出した時刻を$t=0$，物体を投げ出した位置を$\overrightarrow{r}(0)=(0,0)$とする。初速度$\overrightarrow{v}(0)=(v_0,0)$である。$x$軸方向には正の向きに速さ$v_0$の等速度運動，$y$軸方向には初速度０，正の向きに加速度$g$の等加速度運動をするから，時刻$t$における物体の加速度$\overrightarrow{a}=(\frac{d{v}_x}{dt},\frac{d{v}_y}{dt})$は

$\overrightarrow{a}=(0,g)$.

したがって，(1.12)より

$\overrightarrow{v}(t)=\overrightarrow{v}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{a}dt=(v_0,gt).(\because v_x(t)=v_0+\underset{0}{\overset{t}{\int }}0dt=v_0,v_y(t)=0+\underset{0}{\overset{t}{\int }}gdt=gt)$

これを(1.9)に代入すると

$\overrightarrow{r}(t)=\overrightarrow{r}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{v}(t)dt=(v_{0}t,\frac{1}{2}g{t}^2).(\because x(t)=0+\underset{0}{\overset{t}{\int }}{v}_{0}dt=v_{0}t,y(t)=0+\underset{0}{\overset{t}{\int }}gtdt=\frac{1}{2}g{t}^2)$

以上より

$v_x=v_0$

$v_y=gt$

$x=v_{0}t$ (1.13)

$y=\frac{1}{2}g{t}^2$ (1.14)

となる。(1.13)より

$t=\frac{x}{v_0}$

となり，(1.14)に代入すると

$y=\frac{1}{2}g{\left(\frac{x}{v_0}\right)}^2=\frac{g{x}^2}{2v_0^2}$ (1.15)

が得られる。

斜方投射

斜方投射

物体を斜め向きに投げ出すことを斜方投射という。

図のように物体を初速度の大きさ$v_0$で斜め上向きに投げ出す場合を考える。初速度の水平成分の向きに$x$軸，鉛直上向きに$y$軸をとり，時刻$t$における物体の位置を$\overrightarrow{r}(t)=(x(t),y(t))$，速度を$\overrightarrow{v}(t)=(v_x(t),v_y(t))$とする。物体を投げ出した時刻を$t=0$，物体を投げ出した位置を$\overrightarrow{r}(0)=(0,0)$とする。初速度$\overrightarrow{v}(0)=(v_0\cos \theta ,v_0\sin \theta )$である。$x$軸方向には正の向きに速さ$v_0\cos \theta$の等速度運動，$y$軸方向には初速度$v_0\sin \theta$，加速度$-g$の等加速度運動をするから，時刻$t$における物体の加速度$\overrightarrow{a}=(\frac{d{v}_x}{dt},\frac{d{v}_y}{dt})$は

$\overrightarrow{a}=(0,-g)$.

したがって，(1.12)より

$\overrightarrow{v}(t)=\overrightarrow{v}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{a}dt=(v_0\cos \theta ,v_0\sin \theta -gt).(\because \begin{array}{c}{v}_x(t)=v_0\cos \theta +\underset{0}{\overset{t}{\int }}0dt=v_0\cos \theta ,\\ v_y(t)=v_0\sin \theta -\underset{0}{\overset{t}{\int }}gdt=v_0\sin \theta -gt\end{array})$

これを(1.9)に代入すると

$\overrightarrow{r}(t)=\overrightarrow{r}(0)+\underset{0}{\overset{t}{\int }}\overrightarrow{v}(t)dt=(v_{0}t\cos \theta ,v_{0}t\sin \theta -\frac{1}{2}g{t}^2).(\because \begin{array}{c}x(t)=0+\underset{0}{\overset{t}{\int }}{v}_0\cos \theta dt=v_{0}t\cos \theta ,\\ y(t)=0+\underset{0}{\overset{t}{\int }}(v_0\sin \theta -gt)dt=v_{0}t\sin \theta -\frac{1}{2}g{t}^2\end{array})$

以上より

$v_x=v_0\cos \theta$

$v_y=v_0\sin \theta -gt$

$x=v_{0}t\cos \theta$ (1.16)

$y=v_{0}t\sin \theta -\frac{1}{2}g{t}^2$ (1.17)

となる。(1.16)より

$t=\frac{x}{v_0\cos \theta }$

となり，(1.17)に代入すると

$y=v_0\frac{x}{v_0\cos \theta }\sin \theta -\frac{1}{2}g{\left(\frac{x}{v_0\cos \theta }\right)}^2=x\tan \theta -\frac{g{x}^2}{2(v_0\cos \theta {)}^2}$ (1.18)

が得られる。

(1.15), (1.18)より水平投射された物体や斜方投射された物体の軌跡は放物線になることがわかる。このような運動を放物運動という。

力と運動

力

物理において，力とは物体を変形させたり物体の速度を変えたりする働きのことである。力の働きは，大きさ・向き・作用点の３つで決まり，これらを力の３要素という。力の大きさの単位にはニュートン(N)を用いる。

なお，本頁では都合上，重力・張力・抗力・弾性力などの力については「様々な力と運動」の節で，作用・反作用については「運動の法則」の節で扱う。

力の合成と分解

ある物体に向きの違う力$F_1$(青矢印)と力$F_2$(青矢印)を加えると物体に加わる合力は図のような($F_1,F_2$を辺とする)平行四辺形の対角線の向きになる。

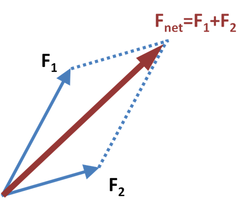
力の合成

１物体にいくつかの力が同時に働くとき，それらの力を合わせた働きをする１つの力を考えることができる。この力を合力といい，合力を求めることを力の合成という。

同一作用線上の同じ向き，又は逆向きの２力$\overrightarrow{F_1},\overrightarrow{F_2}$の合力$\overrightarrow{F}$の大きさはそれぞれの力の大きさの和や差で求められる。また，異なる方向に働く２力$\overrightarrow{F_1},\overrightarrow{F_2}$の合力$\overrightarrow{F}$は２力のベクトルを隣合う２辺とする平行四辺形の対角線の矢印に一致する。これを力の平行四辺形の法則といい，このように求めた２力$\overrightarrow{F_1},\overrightarrow{F_2}$の合力$\overrightarrow{F}$は次式で表される。

$\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}$.

力の分解

2力の分解

１力をそれと同じ働きをするいくつかの力の組に分けることができる。これを力の分解といい，分けられたそれぞれの力を分力という。

力の平行四辺形の法則を用いて，１力$\overrightarrow{F}$は任意方向の２力に分解できる。これを繰り返すと，１力を任意方向のいくつかの力に分解できる。力を分解する場合，互いに垂直な２方向に分解することが多い。力$\overrightarrow{F}$を$x$軸，$y$軸の二方向に分解し，それぞれの分力を$\overrightarrow{F_x},\overrightarrow{F_y}$とする。これらの大きさの向きを表す正負の符号をつけたものを，$\overrightarrow{F}$の$x$成分，$y$成分といい，それぞれ$F_x,F_y$と表す。このとき，$\overrightarrow{F}$の大きさを$F,\overrightarrow{F}$と$x$軸とのなす角を$\theta$とすると

$F_x=F\cos \theta ,F_y=F\sin \theta ,F=\sqrt{{F_x}^2+{F_y}^2}$.

力のつり合い

２力のつり合い

2力のつりあい

物体に２力$\overrightarrow{F_1},\overrightarrow{F_2}$が働いてつり合うとき，２力は同一作用線上にあり，大きさが等しく逆向きであるから

$\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{0}$.

このことから，２力がつり合うときは，２力の合力は$\overrightarrow{0}$であることがわかる。

運動の法則

運動の第１法則 慣性の法則

物体に力が働かぬか，又は力がつりあっているとき，その物体は静止又は等速直線運動を続ける。これを慣性の法則と呼ぶ。

運動の第２法則 運動の法則

質量$m$の物体に働く外力の和が$\overrightarrow{F}$のとき，物体に生ずる加速度を$\overrightarrow{a}$とすると，次の運動方程式が成り立つ。

$m\overrightarrow{a}=\overrightarrow{F}.(\iff \overrightarrow{F}=m\overrightarrow{a})$ (2.1)

なお，(1.4)をを用いて，運動方程式は

$m\frac{d\overrightarrow{v}}{dt}=\overrightarrow{F}$ (2.1)${\displaystyle }$

$m\frac{d^2\overrightarrow{r}}{d{t}^2}=\overrightarrow{F}$ (2.1)${\displaystyle }$

とも表される。

運動の第３法則 作用・反作用の法則

２物体A, Bが互いに力を及ぼしあっている(相互作用をしている)とき，

$f_{\mathrm{A}\mathrm{B}}=$BがAに及ぼす力

$f_{\mathrm{B}\mathrm{A}}=$AがBに及ぼす力

として

$f_{\mathrm{A}\mathrm{B}}=-f_{\mathrm{B}\mathrm{A}}$ (2.2)

が成り立つ。つまり，AがBに及ぼす力とBがAに及ぼす力は大きさが等しくて向きが逆である。

単位と次元

単位

物理量はすべて，基準量の何倍かを表す数値に単位記号を付けて表す。即ち次の関係がある。

物理量＝数値×単位.

力学ではMKS単位系が用いられており，長さはm(メートル)，質量はkg(キログラム)，時間はs(秒)を基本単位として定めている。この３単位に物理学など科学分野や技術分野で用いられる４単位(電流はA(アンペア)，温度はK(ケルビン)，物質量はmol(モル)，光度はcd(カンデラ))を加えた合計７単位を基本単位として定めたのが国際単位系(SI)である。また，基本単位から導かれる単位を誘導単位(組立単位)とよぶ。

様々な力と運動

キログラム原器。米国で保管されているキログラム原器の複製品の画像。フランスの国際キログラム原器と共通化している。

重力

地球上の全物体には，地球が鉛直下向きに引く力，重力が働いている。質量を$m$〔kg〕，重力加速度の大きさを$g$〔m/s$2^{}$〕，重力の大きさ(重さないし重量)を$W$〔N〕とすると，(2.1)より

$mg=W\therefore W=mg$ (2.3)

となる。つまり，重力の大きさは質量に比例し，質量$m$〔kg〕の物体に働く重力の大きさ$W$〔N〕は$mg$〔N〕である。地球上において重力加速度の大きさ$g$は約9.8m/s$2^{}$なので，質量1kgの物体に働く重力の大きさは約9.8Nである。なお，重力加速度の大きさは惑星によっても異なるし，同じ惑星においても緯度により若干変わる。

質量

(2.3)より質量は物体に力が働いた場合の加速度の生じにくさ，即ち慣性の大きさを表す量(慣性質量)であることが分かる。質量は物体固有の量であり，場所によらない。質量の単位である1kgは，国際度量衡局にある国際キログラム原器の質量と定められていたが，2019年５月からプランク定数とよばれる普遍的な定数に基づく定義へと変更された。

束縛力

糸の張力や面の抗力といわれる力は構成している分子間力の合力であるが，通常は伸びぬ糸の張力や固い面が接している物体に及ぼす抗力等は束縛力(拘束力)とよばれ，その大きさは束縛条件(拘束条件)を使って運動方程式を解いてみねば分からぬ未知数として扱われる。

張力

図１

図２

図１のように質量$m$の物体に鉛直下向きに重力$mg$，鉛直上向きに伸び縮みのない糸が物体を引く力(張力)$T$が働いており，物体の加速度を鉛直上向きに$a$とすると，運動方程式は

$ma=T-mg$.

続いて，図２のように水平でなめらかな机上に質量$M$の台車があり，その台車に質量の無視できる糸がつながれ，滑車を介して糸の先に質量$m$の小物体が吊り下げられている場合を考えよう。台車の加速度の大きさを$a$とおくと，束縛条件より小物体の加速度の大きさも$a$である。台車が受ける垂直抗力の大きさを$N$とおくと，台車の運動方程式は(上段が水平方向，下段が鉛直方向)

$\{\begin{array}{c}Ma=T\cdots \cdots (*)\\ M\cdot 0=Mg-N\therefore N=Mg.\end{array}$

小物体の運動方程式は(鉛直方向)

$ma=mg-T.\cdots (**)$

$(*)+(**)$より

$(M+m)a=mg\therefore a=\frac{m}{M+m}g$.

$(*)$に代入

$M\frac{m}{M+m}g=T\therefore T=\frac{Mm}{M+m}g$.

アトウッドの器械

アトウッドの器械で吊り下げられている２物体に対する自由体図(en:free body diagram)。

右図のように質量の無視できる糸の両端に質量$m_1$と質量$m_2$の２物体が滑車を介して吊り下げられている場合を考える(ただし$m_1>m_2$)。重力加速度を$g$とすると，質量$m_1$の物体には鉛直下向きに重力$W_1=m_{1}g$，質量$m_2$の物体には鉛直下向きに重力$W_2=m_{2}g$が働いている。質量$m_1$の物体の加速度の大きさを$a$，質量$m_2$の物体の加速度の大きさを$a^{\prime }$(一応説明のため)，糸の張力の大きさを$T$とおくと，２物体の鉛直方向の運動方程式は

$m_{1}a=m_{1}g-T\cdots \cdots (\mathrm{△})$

$m_2{a}^{\prime }=T-m_{2}g\cdots (◻)$

束縛条件は

$a=a^{\prime }.\cdots \cdots (★)$

$(★)$より，質量$m_2$の物体の加速度の大きさは$a$である(実際はこの程度の束縛条件は自明で最初から$a$としてしまって構わない)。よって，$(◻)$は

$m_{2}a=T-m_{2}g.\cdots (◻{)}^{\prime }$

$(\mathrm{△})+(◻{)}^{\prime }$より

$(m_1+m_2)a=(m_1-m_2)g\therefore a=\frac{m_1-m_2}{m_1+m_2}g$.

$(\mathrm{△})$に代入

$m_1\frac{m_1-m_2}{m_1+m_2}g=m_{1}g-T⟺T=2\frac{m_1{m}_2}{m_1+m_2}g$.

抗力

静止摩擦力と抗力

面や線に沿って運動する物体に面又は線が及ぼす力を面又は線の抗力という。抗力の面に垂直な成分或いは法線方向の分力を垂直抗力，面に平行な成分或いは接線方向の分力を摩擦力という。

静止摩擦力

静止摩擦力は，静止している物体を外から引く力に応じてその大きさを変化させ，摩擦がなかったならば物体が行うであろう運動を妨げる向きに働く。その最大値を最大静止摩擦力或いは最大摩擦力といい，最大摩擦力の大きさは垂直抗力に比例することが分かっている。静止摩擦力，最大摩擦力の大きさをそれぞれ$F,F_{\mathrm{m}\mathrm{a}\mathrm{x}}$，静止摩擦係数を$\mu$，垂直抗力の大きさを$N$とおくと

$F\leqq F_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mu N$. (2.4)

動摩擦力

動摩擦力

物体を引く力と、摩擦力との関係

物体に働く外力が最大摩擦力を越えると，動摩擦力が働く。動摩擦力は物体の運動を妨げる向きに働き，その大きさは垂直抗力に比例する。動摩擦力を$F^{\prime }$，動摩擦係数を${\mu }^{\prime }$とおくと

$F^{\prime }={\mu }^{\prime }N$. (2.5)

なお，動摩擦係数は静止摩擦係数より小さい，即ち動摩擦力は最大摩擦力より小さいことが分かっている。

弾性力

フックの法則

フックの法則

フックの法則

ばねに何も力が加わっていないときのばねの長さをばねの自然長という。一端を固定したばねの他端にばねが伸びる方向に力を加えるとばねは伸び，逆にばねが縮む方向に力を加えるとばねは縮む。その際ばねは自然長に戻ろうとする性質があり，このような力を加えたときに生じた変形が力を加えるのを止めると元に戻る性質を弾性(テンプレート:Lang-en-short)という。この弾性に基づいて生ずる力を弾性力(テンプレート:Lang-en-short)という。ばね弾性力はばねの両端で，自然長に向かう向きに働き，その大きさはばねが自然長から伸び縮みした距離に比例しこれをフックの法則(テンプレート:Lang-en-short)という。ばねが伸びる方向に$x$軸をとり，ばねの自然長の位置を原点にし，ばねの位置を$x$〔m〕，ばね定数を$k$〔N/m〕とすると，ばねの弾性力$F$〔N〕は

$F=-kx$. (2.6)

なお，これは復元力ともよばれる。また，ばねの伸び縮みがあまりにも大きくなるとこれは成り立たなくなる。

圧力

単位面積あたりに垂直に加わる力を圧力(テンプレート:Lang-en-short)という。面積$S$[m$2^{}$]の面に対して垂直に大きさ$F$[N]の力が加わるとき，圧力を$P$[Pa又はN/m$2^{}$]とおくと

$P=\frac{F}{S}$ (2.7)

である。単位のPaはパスカルといい，1Pa＝1N/m$2^{}$である。

水圧

水圧の説明図。水深が深くなるほど、比例して水圧が強くなる。水圧の方向は、物体の面に垂直方向に働く。

水による圧力を静水圧又は水圧という。空気や水のような気体や液体はまとめて流体といい，静止流体中の任意の点を通る１つの面を考えるとき，この面についてのその点の静水圧はつねに面に垂直な圧力で，しかも同一の点では考える面の向きによらず等しい圧力を持つ。

水圧，大気圧をそれぞれ$p,p_0$，水の密度を$\rho$とおく。水中の鉛直方向の長さ$dz$，底面積$A$の微小円柱における力のつり合いは，鉛直下向きを正とすると

$0=pdA-(p+\frac{dp}{dz}dz)dA+\rho gdAdz⟺\frac{dp}{dz}dzdA=\rho gdAdz$

$\therefore \frac{dp}{dz}=\rho g$.

両辺を$z$で積分すると

$\int \frac{dp}{dz}dz=\int \rho gdz⟺p=\rho gz+C$ ($C$は積分定数)

水の表面，すなわち$z=0$において$p_0=\rho g\cdot 0+C⟺C=p_0$であるから上式に代入して深さ$h$，すなわち$z=h$における水圧は

$p=p_0+\rho gh$ (2.8)

である。

浮力

プールに入ると，体が軽くなったように感ずることがある。流体の内部にある物体の表面には流体からの圧力が作用する。圧力は深い程大きいから流体中の物体に作用する圧力の合力は上向きになり，この合力を浮力(テンプレート:Lang-en-short)という。浮力は物体のところにあった流体に作用する重力とつり合っていたので，一般に流体中の物体に作用する浮力の大きさはその物体が押しのけた流体に作用する重力の大きさに等しい。これをアルキメデスの原理(テンプレート:Lang-en-short)という。

抵抗力と終端速度

実際の身の回りの運動では空気抵抗が無視できぬことが多い。空気や水など流体の抵抗とは流体中で物体の運動を妨げる向きに作用する力のことを指す。物体の速さが小さな間は流体中を運動する物体の受ける抵抗力の大きさ$F$は速さ$v$に比例するから

$F=kv$ ($k$は定数) (2.9)

と表せる。速さ$v$に比例する抵抗を粘性抵抗という。

以下では風のない空気中を時刻$t$における速さ$v(t)$に比例する抵抗力$kv(t)$を受けながら鉛直下方に落下する質量$m$の物体の運動を考える。鉛直下向きに$y$軸をとり，重力加速度の大きさを$g$とおくと，物体の運動方程式は

$m\frac{dv(t)}{dt}=mg-kv(t)$

$\begin{array}{cc}\therefore \frac{dv(t)}{dt}& =g-\frac{k}{m}v(t)\\ & =\frac{k}{m}(\frac{mg}{k}-v(t))\therefore \frac{1}{\frac{mg}{k}-v(t)}\cdot \frac{dv(t)}{dt}=\frac{k}{m}.\end{array}$

両辺を時刻$t$で積分すると

$\int \frac{1}{\frac{mg}{k}-v(t)}\cdot \frac{dv(t)}{dt}dt=\int \frac{k}{m}dt$

$⟺\int \frac{dv(t)}{\frac{mg}{k}-v(t)}=\frac{k}{m}t$

$\therefore -\log |\frac{mg}{k}-v(t)|=\frac{k}{m}t+C$. ($C$は積分定数)

物体は鉛直下向きに加速するから$\frac{mg}{k}-v(t)>0$より

$\begin{array}{cc}\log (\frac{mg}{k}-v(t))=-\frac{k}{m}t-C& ⟺\frac{mg}{k}-v(t)=e^{-\frac{k}{m}t-C}\\ & ⟺v(t)=\frac{mg}{k}-e^{-\frac{k}{m}t-C}.\end{array}$

ここで$e^{-C}=A$とおくと

$v(t)=\frac{mg}{k}-A{e}^{-\frac{k}{m}t}$. (2.10)

$t=0$において(境界条件)

$v(0)=\frac{mg}{k}-A{e}^{-\frac{k}{m}0}⟺A=\frac{mg}{k}.(\because v(0)=0)$

これを(2.10)に代入して

$v(t)=\frac{mg}{k}(1-e^{-\frac{k}{m}t})$. (2.11)

したがって終端速度(テンプレート:Lang-en-short)は

$\underset{t\to \mathrm{\infty }}{\lim }v(t)=\frac{mg}{k}$. (2.12)

ちなみにこの物体の時刻$t$における物体の位置は

$\begin{array}{cc}y(t)& =y(0)+\underset{0}{\overset{t}{\int }}v(t)dt\\ & =y(0)+\underset{0}{\overset{t}{\int }}\{\frac{mg}{k}(1-e^{-\frac{k}{m}t})\}dt\\ & =y(0)+\frac{mg}{k}{[t+\frac{m}{k}{e}^{-\frac{k}{m}t}]}_0^t\\ & =y(0)+\frac{mg}{k}(t+\frac{m}{k}{e}^{-\frac{k}{m}t}-\frac{m}{k}).\end{array}$

雨は地上より非常に高いところから降ってくるが，雨滴の速さが大きくなり過ぎぬのはかなり上空で既に終端速度に達しているからと考えられる。

仕事とエネルギー

仕事

物理では，物体に力を加えて動かしたとき，力は物体に対して「仕事をした」という。

運動エネルギー

運動エネルギーと仕事(１次元)

１次元空間($x$軸上)の運動を考える。運動方程式

$m\frac{dv}{dt}=F$ (2.1)${\displaystyle }$

に$v=\frac{dx}{dt}$を掛けて

$mv\frac{dv}{dt}=F\frac{dx}{dt}$.

両辺を$t=t_1$から$t=t_2$まで積分すると

$\underset{t_1}{\overset{t_2}{\int }}mv\frac{dv}{dt}dt=\underset{t_1}{\overset{t_2}{\int }}F\frac{dx}{dt}dt\therefore \underset{t_1}{\overset{t_2}{\int }}mvdv=\underset{t_1}{\overset{t_2}{\int }}Fdx$.

時刻$t=t_1$のとき$v=v_1,x=x_1$，時刻$t=t_2$のとき$v=v_2,x=x_2$と考えて$\begin{array}{cc}t& t_1\to t_2\\ v& v_1\to v_2\\ x& x_1\to x_2\end{array}$とすると

$\underset{v_1}{\overset{v_2}{\int }}mvdv=\underset{x_1}{\overset{x_2}{\int }}Fdx\therefore \frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2=\underset{x_1}{\overset{x_2}{\int }}Fdx$. (3.1)(≪注≫ $F$は一定とは限らぬから右辺は積分実行できない)

この$\frac{1}{2}m{v}^2$を運動エネルギー(テンプレート:Lang-en-short)という。特に，力$F$が一定のとき

$\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2=F(x_2-x_1)$. (3.1a)

(3.1)の右辺は力$F$のした仕事を表している。ゆえに(１次元においては)運動エネルギー変化は仕事に等しい（エネルギーの原理）という因果関係が分かる。

運動エネルギーと仕事(２・３次元)

力が一定の場合

力の向きと動かす向きが違う場合

まず力$\overrightarrow{F}$が一定の場合を考える。時刻$t$において速度$\overrightarrow{v}(t)$で運動する質量$m$の物体の運動方程式

$m\frac{d\overrightarrow{v}(t)}{dt}=\overrightarrow{F}\therefore \frac{d\overrightarrow{v}(t)}{dt}=\frac{\overrightarrow{F}}{m}=$一定．

これと(1.12)より時刻$0\sim t$における運動エネルギー変化はこの間の物体の変位を$\mathrm{\Delta }\overrightarrow{r}=\overrightarrow{r}(t)-\overrightarrow{r}(0)$として

$\begin{array}{cc}\frac{1}{2}m\overrightarrow{v}(t{)}^2-\frac{1}{2}m\overrightarrow{v}(0{)}^2& =\frac{1}{2}m{(\overrightarrow{v}(0)+\underset{0}{\overset{t}{\int }}\frac{d\overrightarrow{v}(t)}{dt}dt)}^2-\frac{1}{2}m\overrightarrow{v}(0{)}^2\\ & =\frac{1}{2}m\{2\overrightarrow{v}(0)\frac{d\overrightarrow{v}(t)}{dt}t+{\left(\frac{d\overrightarrow{v}(t)}{dt}t\right)}^2\}\\ & =m\frac{d\overrightarrow{v}(t)}{dt}\cdot (\overrightarrow{v}(0)t+\frac{1}{2}\frac{d\overrightarrow{v}(t)}{dt}{t}^2)\\ & =m\frac{d\overrightarrow{v}(t)}{dt}\cdot (\overrightarrow{r}(t)-\overrightarrow{r}(0))=\overrightarrow{F}\cdot \mathrm{\Delta }\overrightarrow{r}.(3.2)\end{array}$

ここで$\overrightarrow{F}$と$\mathrm{\Delta }\overrightarrow{r}$とのなす角を$\theta$とすると，この間に力$\overrightarrow{F}$がした仕事$W$は

$W=\overrightarrow{F}\cdot \mathrm{\Delta }\overrightarrow{r}=|\overrightarrow{F}||\mathrm{\Delta }\overrightarrow{r}|\cos \theta$ (3.2a)

と与えられる。なお仕事の単位はJ=N・mである(ジュール)。

位置エネルギー

仕事が始点と終点のみで決まり，経路によらぬ力を保存力(テンプレート:Lang-en-short)(例：重力，弾性力，万有引力，静電気力等)，その他の力(仕事が経路による力)を非保存力(例：摩擦力等)という。 保存力の場合，始点$\overrightarrow{r_0}$を決めるとその始点$\overrightarrow{r_0}$を基準とした終点$\overrightarrow{r}$での保存力$\overrightarrow{f_{\mathrm{C}}}$の位置エネルギー(テンプレート:Lang-en-short)$U(\overrightarrow{r})$が決まる。

$U(\overrightarrow{r})=-\underset{\overrightarrow{r_0}}{\overset{\overrightarrow{r}}{\int }}\overrightarrow{f_{\mathrm{C}}}\cdot d\overrightarrow{r}$. (3.3)

重力による位置エネルギー

鉛直上方に$y$軸をとり，$y=0$の点を基準とした$y=h$での質量$m$の物体の位置エネルギー$U$は，重力加速度を$g$とすると，重力は$-mg$であるから

$U=-\underset{0}{\overset{h}{\int }}(-mg)dy=mgh$. (3.4)

また，時刻$t$において$y=y(t)$の位置にある質量$m$の物体の時刻$t=0$から$t=t$までの位置エネルギー変化$\mathrm{\Delta }U$は，重力加速度を$g$とすると

$\mathrm{\Delta }U=-\underset{y(0)}{\overset{y(t)}{\int }}(-mg)dy=mg(y(t)-y(0))$. (3.4a)

弾性力による位置エネルギー

弾性力と位置エネルギー

弾性エネルギーの差

右図のように壁に取付けられたばね定数$k$のばねにつながれた質量$m$の物体において，水平方向右向きに$x$軸をとり，ばねの長さが自然長のときの物体の位置を原点とする。物体が$x$の位置にあるとき，運動方程式

$m\frac{d^{2}x}{d{t}^2}=-kx$.

よって，原点を基準とした位置$x$での物体の位置エネルギー$U$は

$U=-\underset{0}{\overset{x}{\int }}(-kx)dx=\frac{1}{2}k{x}^2$. (3.5)

なお，この弾性力による位置エネルギーを弾性エネルギー(テンプレート:Lang-en-short)ともいう。また，時刻$t$において$x=x(t)$の位置にある質量$m$の物体の時刻$t=0$から$t=t$までの位置エネルギー(弾性エネルギー)変化$\mathrm{\Delta }U$は

$\mathrm{\Delta }U=-\underset{t_1}{\overset{t_2}{\int }}(-kx(t))dx=\frac{1}{2}kx(t_2{)}^2-\frac{1}{2}x(t_1{)}^2$. (3.5a)

力学的エネルギー保存

落下運動と力学的エネルギー

運動エネルギーと位置エネルギーの和を力学的エネルギー(テンプレート:Lang-en-short)という。運動エネルギー，位置エネルギー，力学エネルギーをそれぞれ$K,U,E$とおくと

$E=K+U$. (3.6)

右図のように質量$m$の物体を地上からの高さ$h_2$から高さ$h_1$まで落下させるとする。物体には鉛直下向きに重力$mg$(保存力)が働いている。(3.1a)より

$\frac{1}{2}m{v_1}^2-\frac{1}{2}m{v_2}^2=-mg(h_1-h_2)⟺\frac{1}{2}m{v_1}^2+mg{h}_1=\frac{1}{2}m{v_2}^2+mg{h}_2$.

上式の同値変形後の式を見ると，$h_1$地点での物体の運動エネルギーと位置エネルギーの和が$h_2$地点での物体の運動エネルギーと位置エネルギ－の和が等しい，すなわち保存力場での質点の運動は力学的エネルギーが一定であることが分かる。

$E=K+U=$一定．(3.7)

これを力学的エネルギー保存則(テンプレート:Lang-en-short)という。