初等幾何学/図形の基本

三角形

三角形の合同

$\mathrm{△}ABC,\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ について、

$\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime },\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime },\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime },AB=A^{\prime }{B}^{\prime },BC=B^{\prime }{C}^{\prime },CA=C^{\prime }{A}^{\prime }$

が成り立つとき、この2つの三角形を合同である、と言い、$\mathrm{△}ABC\equiv \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ と表す。

直観的な意味は、平行移動、回転、反転すれば三角形が完全に一致するということである。

さて、2つの三角形が合同であることを言うには 6 もの条件が必要である。しかし、三角形の合同条件というものがあり、半分の条件で済むようになっている。

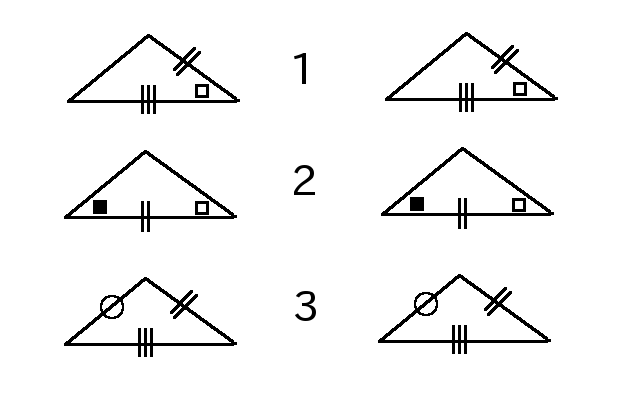
1. 二辺夾角相等
2. 二角夾辺相等
3. 三辺相等

$\mathrm{△}ABC,\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ について、

1. $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime },AB=A^{\prime }{B}^{\prime },AC=A^{\prime }{C}^{\prime }$
2. $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime },\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime },AB=A^{\prime }{B}^{\prime }$
3. $AB=A^{\prime }{B}^{\prime },BC=B^{\prime }{C}^{\prime },CA=C^{\prime }{A}^{\prime }$

のいずれかが成り立てば三角形は合同であると言える。図にすると以下の通り。

相似

$\mathrm{△}ABC,\mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$ について、

$\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime },\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime },\mathrm{\angle }C=\mathrm{\angle }{C}^{\prime }$

が成り立つとき、これを三角形が相似である、という。このとき、

$AB:BC:CA=A^{\prime }{B}^{\prime }:B^{\prime }{C}^{\prime }:C^{\prime }{A}^{\prime }$ が成り立つ。

相似条件には合同条件と似たものがある。

1. 二角相等
2. 二辺比夾角相等
3. 三辺比相等

それぞれ、

1. $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime },\mathrm{\angle }B=\mathrm{\angle }{B}^{\prime }$
2. $\mathrm{\angle }A=\mathrm{\angle }{A}^{\prime },AB:A^{\prime }{B}^{\prime }=AC:A^{\prime }{C}^{\prime }$
3. $AB:BC:CA=A^{\prime }{B}^{\prime }:B^{\prime }{C}^{\prime }:C^{\prime }{A}^{\prime }$

円

円に関する理論は他のページで進める。

面積・体積

長方形の面積を、縦と横の線分の積と定義し、立方体の体積を、縦と横と奥行きの線分の積と定義する。

面積・体積についてはどちらもカヴァリエリの原理を適応する。すなわち、高さが等しく、切断した線分の長さ・断面積が等しければ体積は等しいとする。